Wendepunkte mit der dritten Ableitung nachweisen
Bei einfachen Lösungen der Gleichung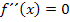 
liegt immer ein Vorzeichenwechsel von 
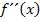vor. Alle Punkte, welche die Gleichung 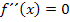erfüllen und wo sich das Vorzeichen von 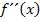ändert, sind Wendepunkte. Deshalb ist bei einer einfachen Lösung wirklich ein Wendepunkt. Bei doppelten Lösungen der Gleichung 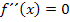liegt grundsätzlich kein Vorzeichenwechsel von 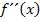vor. Deshalb ist bei einer doppelten Lösung kein Wendepunkt.
2. Bsp.:
Gegeben ist die Funktionenschar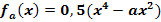 
mit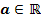 
. Berechne die Flachpunkte der Schar in Abhängigkeit von a! Für welche Werte von a ergeben sich Wendepunkte? Bestimme auch diejenige Funktion der Schar, die bei 
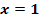einen Wendepunkt besitzt!
Lösung:
Es handelt sich bei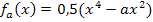 
um eine Funktionenschar. Das erkennt man am Vorkommen des Scharparameters a in der Funktionsgleichung. Wenn man für a verschiedene Werte einsetzt, bekommt man jeweils andere Funktionen, also viele Funktionen, eben eine Schar. In Abhängigkeit von a rechnen, bedeutet, dass man für a nichts einsetzten soll, aber mit a rechnen soll, als wäre es eine konkrete Zahl. Es sollen hier erst einmal alle Flachpunkte in Abhängigkeit von a ermittelt werden, also diejenigen Punkte von 
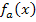, wo gilt:
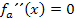
Ob sich das Vorzeichen von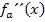 
ändert oder nicht, spielt für die Flachpunkte keine Rolle. Erst bei der Untersuchung auf Wendepunkte wird das wichtig. Wendepunkte sind nur diejenigen Flachpunkte, bei denen sich das Vorzeichen von 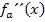ändert. Statt des Vorzeichenwechsels von 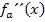an der Stelle 
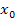kann auch 
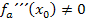verwendet werden, um den Scharparameter a so zu bestimmen, dass es sich bei den Flachpunkten sogar um Wendepunkte handelt. Am Ende der Aufgabe soll diejenige Funktion der Schar ermittelt werden, also ihre Funktionsgleichung aufgestellt werden, die bei 
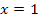einen Wendepunkt hat. Dazu muss a so bestimmt werden, dass bei 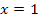ein Wendepunkt liegt. Das geht ganz schnell, denn wir haben vorher schon die x-Koordinate des Wendepunkts in Abhängigkeit von a berechnet. Dies muss nur noch gleich 1 gesetzt werden und nach a aufgelöst werden. Dann setzt man den ermittelten Wert von a in 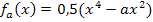ein und schon hat man die gesuchte Funktion. Wenn dir das soweit klar ist, solltest du versuchen, die Aufgabe alleine zu bearbeiten. Ist dir das alles noch nicht so ganz klar, schaust du dir den folgenden Lösungsweg genau an und versuchst die Aufgabe später noch einmal nachzurechnen. Los geht´s!
Wir bilden vorweg die ersten drei Ableitungen mit der Regel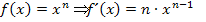 
. Achtung:Wir leiten nach x ab!
