Wendepunkte mit der dritten Ableitung nachweisen
1. Bsp.:
Gegeben ist die Funktion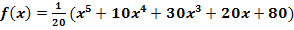 
. Ihr Graph wird mit 
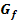bezeichnet.
Berechne die Koordinaten aller Flachpunkte von 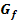! Handelt es sich dabei auch um Wendepunkte?
Lösung:
Vorweg bilden wir die ersten drei Ableitungen.
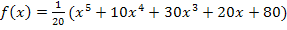
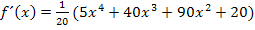
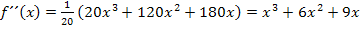
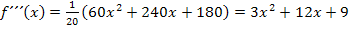
(Wenn dir nicht klar ist, wie man auf die Ableitungen kommt, arbeite unbedingt erst den Teil Einfache Ableitungsregelndurch!)
Nun berechnen wir die Flachpunkte. Flachpunkte heißen ja all diejenigen Punkte, wo der Funktionsgraph die Krümmung Null besitzt. Die Krümmung von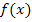 
entspricht der zweiten Ableitung 
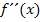. Wir setzen daher die zweite Ableitung gleich Null und lösen nach x auf.
FLAP: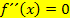 
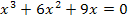
Dies ist eine Gleichung dritten Grades. Sie lässt sich leicht lösen, indem man x ausklammert.
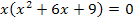
Durch das Ausklammern ist eine Gleichung der Form „Produkt = 0“ entstanden. Ein Produkt ist bekanntlich gleich Null, wenn einer der Faktoren gleich Null ist. Deshalb darf man die Faktoren jeweils einzeln gleich Null setzen.
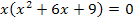
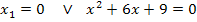
Um die hintere Gleichung zu lösen, kann die Mitternachtsformel angewendet werden.
Zur Erinnerung: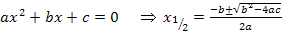 
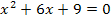
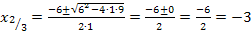
Da die Diskriminante, also der Ausdruck unter der Wurzel bei der Mitternachtsformel, hier gleich Null ist, fallen die Lösungen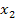 
und 
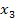zusammen. Es handelt sich bei 
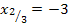um eine doppelte Lösung. Im Gegensatz dazu ist die andere Lösung 
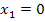eine einfache Lösung.
Die Gleichung 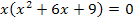hätte sich aber auch schneller lösen lassen. Der Ausdruck 
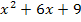stellt nämlich eine binomische Formeldar. Genauer gesagt handelt es sich dabei um die erste binomische Formel:
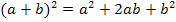
Wenn man das erkennt, kann man sich die Mitternachtsformel sparen und nach folgendem Weg vorgehen:
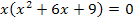
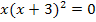
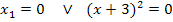
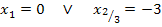
Dass es sich bei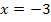 
um eine doppelte Lösung handelt, erkennt man bei 
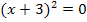an dem Quadrat außerhalb der Klammer. Beim ersten Faktor x steht dagegen keine Potenz, daher ist 
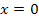eine einfache Lösung der Gleichung.
Berechnung der zugehörigen y-Koordinaten:
Einsetzten der x-Koordinaten in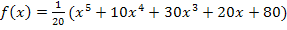
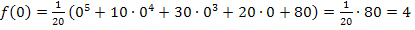
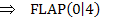
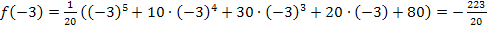
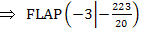
Überprüfung, ob es sich bei den ermittelten Flachpunkten auch um Wendepunkte handelt:
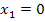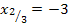Wir setzten die x-Koordinaten und in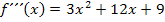 
ein. Ergibt sich dabei nicht Null, handelt es sich an der jeweiligen Stelle um einen Wendepunkt.
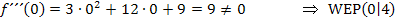
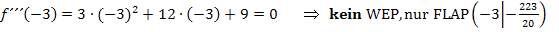
Wir stellen fest:Bei der einfachen Lösung 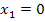liegt eine Wendestelle vor, bei der doppelten Lösung 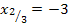dagegen nicht.
Es ist generell so, dass es sich bei einfachen Lösungen der Gleichung 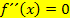immer um Wendepunkte handelt, bei doppelten Lösungen dagegen nicht. Doppelte Lösungen der Gleichung 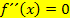sind nur Flachpunkte, aber eben keine Wendepunkte.
