Wendepunkte mit der dritten Ableitung nachweisen
An Stelle des Vorzeichenwechsels von 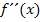 kann natürlich genauso gut gezeigt werden, dass
kann natürlich genauso gut gezeigt werden, dass 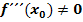 gilt. Auch dann liegt wirklich ein Wendepunkt vor, nicht nur ein reiner Flachpunkt.
gilt. Auch dann liegt wirklich ein Wendepunkt vor, nicht nur ein reiner Flachpunkt.
Ein Wendepunkt ist somit ein Flachpunkt mit Vorzeichenwechsel der Krümmung.
Setzt man die zweite Ableitung gleich Null und löst nach x auf, erhält man die x-Koordinaten aller Punkte, wo der Graph keine Krümmung hat, also aller Flachpunkte – dazu gehören auch die Wendepunkte. Um zu überprüfen, ob einer der ermittelten Flachpunkte auch ein Wendepunkt ist, muss dann allerdings entweder der Vorzeichenwechsel von 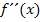 nachgewiesen werden, oder man setzt die ermittelten x-Koordinaten jeweils in die dritte Ableitung ein. Ergibt sich dabei ein Wert ungleich Null, ist an dieser Stelle ein Wendepunkt, ansonsten ist dort nur ein reiner Flachpunkt, aber eben kein Wendepunkt.
nachgewiesen werden, oder man setzt die ermittelten x-Koordinaten jeweils in die dritte Ableitung ein. Ergibt sich dabei ein Wert ungleich Null, ist an dieser Stelle ein Wendepunkt, ansonsten ist dort nur ein reiner Flachpunkt, aber eben kein Wendepunkt.
Vorsicht:Ist in einer Aufgabe nach einem Wendepunkt gefragt, wirklich nicht nur die zweite Ableitung gleich Null setzten und den Punkt berechnen, sondern auch immer zusätzlich nachweisen, dass wirklich ein Wendepunkt vorliegt! D.h. entweder zeigen, dass sich das Vorzeichen von 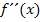 an dieser Stelle ändert oder dass die dritte Ableitung dort ungleich Null ist. Vergisst du den Nachweis des Wendepunktes in einer Prüfung, werden dir hundertprozentig Punkte abgezogen!
an dieser Stelle ändert oder dass die dritte Ableitung dort ungleich Null ist. Vergisst du den Nachweis des Wendepunktes in einer Prüfung, werden dir hundertprozentig Punkte abgezogen!
Wird dagegen nur nach Flachpunkten gefragt, braucht man nur 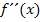 gleich Null zu setzten, nach x auflösen und die zugehörige y-Koordinate berechnen. Fertig! (Dasselbe gilt natürlich auch, wenn in der Aufgabenstellung zwar nach dem Wendepunkt gefragt ist, aber extra der Zusatz „Nachweis nicht verlangt“ in der Aufgabenstellung enthalten ist. Dann kannst du auf den Nachweis natürlich getrost verzichten.)
gleich Null zu setzten, nach x auflösen und die zugehörige y-Koordinate berechnen. Fertig! (Dasselbe gilt natürlich auch, wenn in der Aufgabenstellung zwar nach dem Wendepunkt gefragt ist, aber extra der Zusatz „Nachweis nicht verlangt“ in der Aufgabenstellung enthalten ist. Dann kannst du auf den Nachweis natürlich getrost verzichten.)
Stichpunktartige Zusammenfassung:
Geg.: 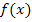
Berechnung der Wendepunkt(e) · · D.h. zweite Ableitung gleich Null setzten und nach x auflösen. Das ergibt die x-Koordinate(n) · D.h. die x-Koordinate(n) des Wendepunktes oder der Wendepunkte jeweils in die Funktionsgleichung · Nachweis des Wendepunktes 1. Möglichkeit:Mit dritter Ableitung
D.h. die x-Koordinate(n) des Wendepunktes oder der Wendepunkte jeweils in die dritte Ableitung 2. Möglichkeit:Mit Untersuchung des Krümmungsverhaltens Wenn ein Vorzeichenwechsel von
|
Schauen wir uns doch ein paar konkrete Aufgabenbeispiele für den Nachweis von Wendepunkten mit der dritten Ableitung an.

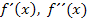 und
und 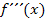 bilden
bilden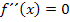
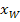 des Wendepunkts oder der Wendepunkte
des Wendepunkts oder der Wendepunkte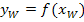
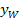 des Wendepunktes oder der Wendepunkte
des Wendepunktes oder der Wendepunkte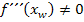
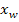 vorliegt, handelt es sich um einen Wendepunkt.
vorliegt, handelt es sich um einen Wendepunkt.