Wendepunkte mit der dritten Ableitung nachweisen
Der Nenner kann sowieso nicht gleich Null werden, da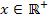 
gilt. Wir können also einfach den Zähler gleich Null setzten.
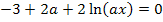
Auf diese Gleichung wärst du natürlich auch gekommen, wenn du einfach auf beiden Seiten der Gleichung mit dem Nenner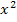 
multipliziert hättest, also das 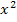auf die andere Seite der Gleichung gebracht hättest. Es gilt schließlich:
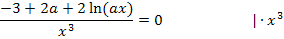
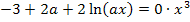
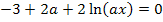
Diese Gleichung lösen wir nun nach x auf, indem wir zuerst den Ausdruck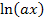 
isolieren und dann den ln mit 
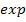, d.h. „e hoch …“ , beseitigen.
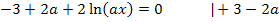
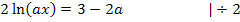
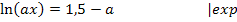
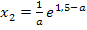
Berechnung der y-Koordinate:
Es wird dazu die x-Koordinate 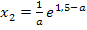in die Funktionsgleichung 
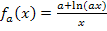eingesetzt.
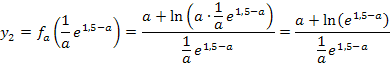
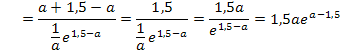
Sollten dir die letzten beiden Umformungen nicht klar sein, überlegst du dir folgendes:Man dividiert durch einen Bruch, indem man mit seinem Kehrwert multipliziert. Man dividiert also durch 
, indem man mit 
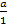, also mit a multipliziert. Deshalb gilt:
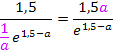
Bei der Umformung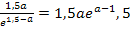 
wurde das Potenzgesetz 
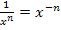verwendet. Das ist nicht so leicht nachzuvollziehen. Daher noch einmal alles ganz langsam.
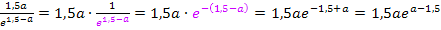
Nun kennen wir die Koordinaten des einzigen Punktes ohne Krümmung, also des einzigen Flachpunktes: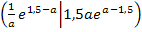 
Ob es sich wirklich um einen Wendepunkt handelt, müssen wir noch zeigen.
Nachweis des Wendepunktes:
Wir setzten dazu die x-Koordinate 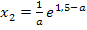in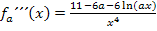 
ein. Ergibt sich dabei ein Wert ungleich Null, liegt ein Wendepunkt vor.
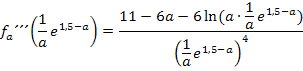
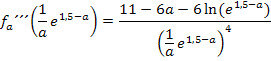
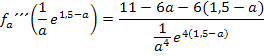
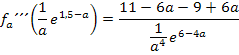
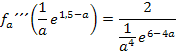
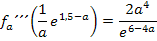
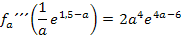
Für beliebige positive Werte von a gilt:
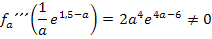
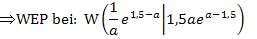
Damit ist bewiesen, dass für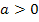 
genau ein Hochpunkt und ein Wendepunkt vorliegen. Fertig!
Manche Lehrer(innen) sprechen in diesem Zusammenhang immer wieder von einer „notwendigen“ und von einer „hinreichenden“ Bedingung für einen Wendepunkt. Was er/sie damit meint, wird im Folgenden erklärt.
Notwendige und hinreichende Bedingung für einen Wendepunkt
Damit an der Stelle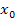 
ganz sicher ein Wendepunkt (WEP) vorliegt und nicht etwa nur ein Flachpunkt, muss neben 
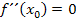auch ein Vorzeichenwechsel von 
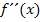an der Stelle 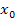vorliegen oder es muss 
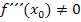gelten. Der Vorzeichenwechsel von 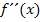oder die Bedingung 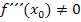ist eine sogenannte „hinreichende“ Bedingung für einen Wendepunkt. Damit meint ein Mathematiker, dass der Vorzeichenwechsel von 
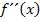oder die Bedingung 
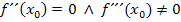ausreichend (hinreichend) sind, damit ganz sicher bei 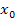ein Wendepunkt vorliegt. Wenn nur die Bedingung 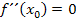erfüllt ist, muss jedoch nicht zwangsläufig ein Wendepunkt vorliegen. 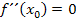bedeutet alleine nur, dass der Funktionsgraph an der Stelle 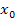die Krümmung 0 hat.
