Wendepunkte mit der dritten Ableitung nachweisen
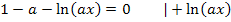
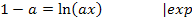
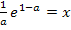
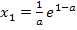
Da für a laut Angabe nur positive Werte eingesetzt werden dürfen, gibt es immer genau einen Punkt mit waagrechter Tangente. (Für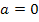 
würde sich keine Lösung ergeben, da die Division durch Null nicht definiert ist. Doch wegen 
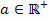kommt dieser Fall sowieso nicht vor.) Nun müssen wir die zugehörige y-Koordinate berechnen und nachweisen, dass es sich für alle 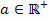wirklich um einen Hochpunkt (HOP) handelt und nicht um einen Tiefpunkt (TIP) oder Terrassenpunkt (TEP).
Berechnung der zugehörigen y-Koordinate:
Es wird dazu die x-Koordinate 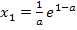in die Funktionsgleichung 
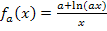eingesetzt.
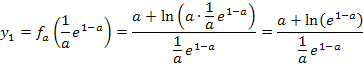
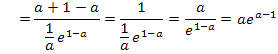
Sollten dir die vorletzte Umformung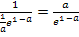 
nicht klar sein, überlegst du dir folgendes:Man dividiert durch einen Bruch, indem man mit seinem Kehrwert multipliziert. Man dividiert also durch 
, indem man mit 
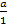, also mit a multipliziert. Deshalb gilt: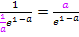 
Bei der letzten Umformung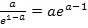 
wurde das Potenzgesetz 
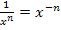verwendet. Das ist nicht so leicht nachzuvollziehen. Daher noch einmal alles ganz langsam.
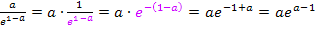
Nun kennen wir die Koordinaten des einzigen Punktes mit waagrechter Tangente: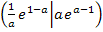 
Überprüfung der Art des Extremums:
Es wird dazu die x-Koordinate 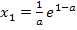in die zweite Ableitung 
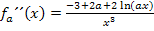eingesetzt und das Vorzeichen bestimmt.
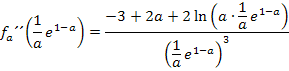
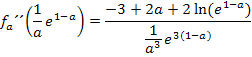
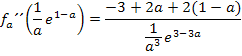
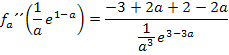
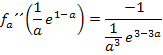
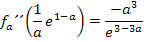
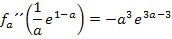
Da a laut Angabe für eine positive Zahl steht, ist der Ausdruck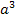 
positiv und entsprechend 
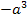negativ. Der Ausdruck 
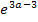ist immer positiv, egal was für a eingesetzt wird. (Denk daran:„e hoch irgendwas ist immer positiv!“) Wegen „Minus mal Plus ist Minus“ ist der gesamte Ausdruck 
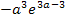daher negativ. Es existiert daher für beliebige (positive) Werte von a genau ein Hochpunkt. Somit ist gezeigt, dass jede Scharkurve genau einen Hochpunkt hat. Weitere Hochpunkte kann es ja nicht geben, da es keine anderen Punkte mit waagrechten Tangenten gibt. Aus 
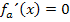ergab sich schließlich nur die einzige Lösung .
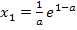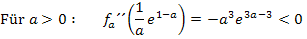
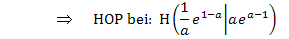
Anmerkung:Für negative Werte von a hätte sich ein Tiefpunkt ergeben, weil sich für a 
bei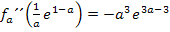 
ein positiver Wert ergeben hätte. Für 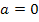hätte sich gar kein Extremum ergeben;die x-Koordinate 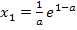wäre für 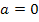schließlich gar nicht definiert. (Division durch Null nicht definiert)
So, den ersten Teil der Aufgabe haben wir gelöst. Nun muss noch gezeigt werden, dass für beliebige positive Werte von a immer genau ein Wendepunkt existiert.
Berechnung des Wendepunktes:
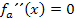
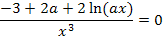
Ein Bruch ist gleich Null, wenn der Zähler gleich Null ist und der Nenner nicht gleich Null ist.
