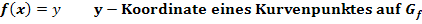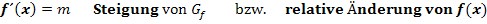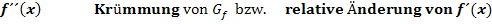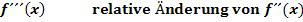Wendepunkte mit der dritten Ableitung nachweisen

Um diesen Teil verstehen zu können, solltest du wissen, was die erste Ableitung 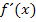und die zweite Ableitung 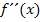einer Funktion 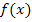bedeuten, und vor allem wie sie gebildet werden. Wenn du das noch nicht weißt, arbeite besser erst die Teile Einfache Ableitungsregelnund Weitere Ableitungsregelnsowie den Teil Zweite Ableitung 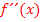durch. (Für Schüler, die noch mehr über die erste Ableitung wissen wollen:Ganz ausführlich wird die erste Ableitung im gesonderten Teil Die Ableitungsfunktion 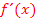behandelt.)

Du weißt:Wendepunkte sind Punkte, wo der Funktionsgraph sein Krümmungsverhalten ändert.

Kurze Wiederholung:

Das Krümmungsverhalten einer Funktion 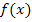wird durch die zweite Ableitung 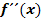beschrieben, es entspricht der relativen Änderung der Steigung.

Die Steigung der Funktion 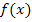wird durch die erste Ableitung 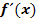beschrieben;dies entspricht der relativen Änderung des y-Wertes .

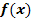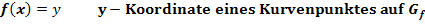
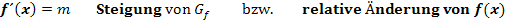
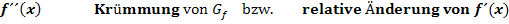
Wo der Funktionsgraph 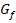beispielsweise steil und in einer engen Kurve (stark gekrümmt) verläuft, ist die Steigung 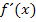vom Betrag her großund auch die Änderung der Steigung, also die Krümmung 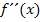ist vom Betrage her groß.

Nun kommt auch noch die dritte Ableitung 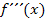hinzu. Was ist 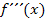anschaulich? Wenn die erste Ableitung 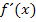die relative Veränderung von 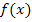darstellt und die zweite Ableitung 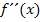die relative Veränderung von 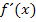, muss wohl entsprechend die dritte Ableitung 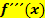die relative Veränderung von 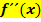sein. Die dritte Ableitung entspricht also der relativen Änderung der Krümmung. Das kann man sich leider nicht mehr so gut vorstellen. Das macht aber nichts. Es reicht aus zu wissen, dass für die dritte Ableitung gilt 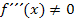, wenn sich die Krümmung 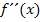beispielsweise vom Vorzeichen her ändert. Liegt umgekehrt keine Änderung der Krümmung vor, gilt 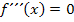. Dieser Zusammenhang kann für den Nachweis eines Wendepunktes verwendet werden.

Noch einmal alles übersichtlich dargestellt:

Im Wendepunkt verläuft der Graph 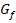lokal am steilsten bzw. flachsten;die Krümmung ist dort gleich Null und ändert auch ihr Vorzeichen. Anschaulich entspricht die Vorzeichenänderung der Krümmung 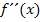dem Umlenken von einer Rechtskurve in eine Linkskurve oder umgekehrt, wenn man sich vorstellt, man würde auf dem Graph 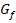entlang fahren. Ein Wendepunkt ist also ein Punkt, wo man „umlenkt“. Da sich im Wendepunkt die Krümmung vom Vorzeichen her ändert, ist die dritte Ableitung – das ist ja die Veränderung der Krümmung – nicht gleich Null. Wäre die dritte Ableitung gleich Null, würde das ja bedeuten, dass es keine Änderung der Krümmung, also auch keinen Vorzeichenwechsel von 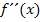gäbe. Dann könnte an dieser Stelle kein Wendepunkt sein.

Bisher haben wir Wendepunkte berechnet, indem wir die zweite Ableitung 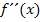gleich Null gesetzt haben. Dann wurde der Vorzeichenwechsel von 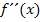gezeigt, um zu beweisen, dass wirklich ein Wendepunkt vorliegt. Dass 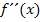am Wendepunkt das Vorzeichen ändert, wurde beispielsweise mit einer Krümmungstabelle gezeigt. Das Anfertigen der Krümmungstabelle dauert jedoch oft sehr lang. Erfreulicherweise kann man mit der dritten Ableitung Wendepunkte viel schneller nachweisen – zumindest dann, wenn sich die Funktion schnell ein drittes Mal ableiten lässt.

---