Kurzwiederholung der grundlegenden Ableitungsregeln

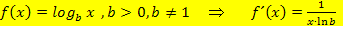(Stoff 11. Klasse G8, 2. Halbjahr)

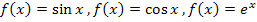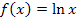Du findest diese Ableitungen auch in deiner Formelsammlung bzw. Merkhilfe. Dennoch empfiehlt es sich, zumindest die Ableitungen der oberen vier Grundfunktionen und auswendig zu lernen, da du sie sehr oft brauchen wirst. (Falls ihr im Unterricht die Funktionen 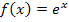und 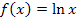noch nicht behandelt habt, überspringst du momentan einfach diejenigen Beispiele, welche oder 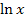enthalten.) Du solltest aber zumindest alle anderen oben aufgeführten Ableitungsregeln sicher beherrschen, bevor du dich mit den neuen Ableitungsregeln (Produkt-, Quotienten- und Kettenregel) beschäftigst.

Außerdem wäre es gut, wenn du die Ableitung der Wurzelfunktion auswendig kannst. Sie steht nicht in der Formelsammlung bzw. Merkhilfe, da man sie mit Hilfe der Potenzgesetze und der Regel 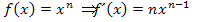eigentlich selbst herleiten kann, doch das dauert einfach zu lange. Besser, du merkst dir:

So kannst du dir diese Formel selbst herleiten:

Bei der „normalen“ Wurzel 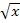handelt es sich genau genommen um die Quadratwurzel aus x, also um die zweite Wurzel 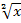. Daher gilt wegen : 

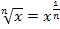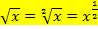
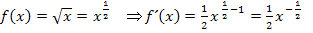
Die Ableitung 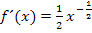lässt sich noch weiter vereinfachen. Letztendlich soll eine Ableitung grundsätzlich keine negativen Zahlen oder Brüche mehr im Exponenten enthalten. Mit der Formel 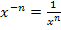und mit 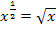kann folgende Umformung gemacht werden:

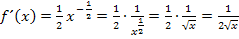
Dies ist die oben bereits gezeigte Ableitung der Wurzelfunktion.

Jetzt aber zu den Ableitungsregeln für Produkte, Quotienten und verketteten Funktionen.

Wir beginnen mit der Einfachsten dieser Regeln, mit der sogenannten Produktregel. Man verwendet sie, wenn man ein Produkt ableiten soll, das in beiden Faktoren die Variable x enthält und das sich gar nicht oder zumindest nicht schnell ausmultiplizieren lässt. Mehr dazu bei:Die Produktregel

Danach geht es weiter mit der Quotientenregel. Damit werden Funktionen abgeleitet, die zumindest im Nenner die Variable x enthalten und die sich auch nicht auf die Form 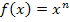bringen lassen. Mehr dazu bei:Die Quotientenregel

Als letzte neue Regel wird die Kettenregel erklärt;sie ist für die meisten Schüler die schwierigste der drei neuen Ableitungsregeln. Die Kettenregel muss beim Ableiten von Funktionen angewendet werden, die ineinander verschachtelt sind, also wenn eine Funktion in eine andere Funktion für x eingesetzt ist. Man nennt dieses Ineinander-Einsetzen mathematisch „Verketten“. Mehr dazu bei:Die Kettenregel

---