Kombinationen der verschiedenen Ableitungsregeln
Zu 9c.)
Hier noch einmal die Angabe: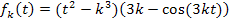 
Die Variable ist hier t und der Parameter k. Es muss also nach t abgeleitet werden. Du musst dich dabei also voll und ganz auf das t konzentrieren! Bei der vorliegenden Funktion handelt es sich um ein Produkt, das in beiden Faktoren die Variable t enthält. Wir müssen daher zum Ableiten die Produktregel verwenden. Der erste Faktor des Produkts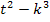 
ergibt nach t abgeleitet 2t. Dabei fällt der Ausdruck 
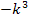weg, weil es sich bei 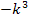um eine additive Konstante handelt;also um eine „Zahl“ ohne t, welche addiert bzw. subtrahiert wird. Solche „Zahlen“ fallen beim Ableiten schließlich immer weg. Entsprechendes gilt beim Ableiten des zweiten Faktors 
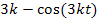für den Ausdruck 3k. Auch das 3k fällt beim Ableiten nach t komplett weg, weil es eine additive Konstante darstellt. Allerdings muss beim Ableiten von 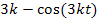die Kettenregel verwendet werden, denn es handelt sich um eine verkettete Funktion. Also beim Ableiten der zweiten Klammer das Nachdifferenzieren nicht vergessen! Die innere Funktion von 
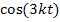ist 3kt. 3kt nach t abgeleitet ergibt 3k. Es muss beim Ableiten von 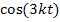laut Kettenregel mit der Ableitung der inneren Funktion, d.h. dann in diesem Fall mit 3k, nachdifferenziert werden.
Jetzt bist du d´ran! Erst selber ableiten und dann weiter lesen!
Zur Kontrolle deines Ergebnisses:
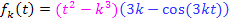
Produktregel:
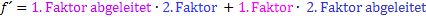
Nachdifferenzieren (laut Kettenregel)
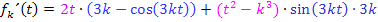
Vereinfachen lässt sich hier nichts. Fertig!
Zu 9d.)
Hier noch einmal die Angabe: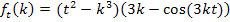 
Nun ist es genau umgekehrt wie bei 9c.):Die Variable ist jetzt k und der Parameter t. Es muss hier also nach k abgeleitet werden. Du musst dich deshalb vor allem auf k konzentrieren. Um die Ableitung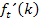 
zu bilden, braucht man zuerst einmal die Produktregel, weil es sich bei 
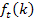um ein Produkt handelt, das die Variable k in beiden Faktoren enthält. Die Ableitung des ersten Faktors 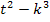zu finden, dürfte für dich an sich kein Problem darstellen: 
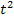stellt dabei eine additive Konstante dar, also quasi eine normale „Zahl“ ganz ohne k. Deshalb fällt das 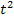beim Ableiten des ersten Faktors komplett weg. 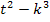ergibt nach k abgeleitet dem entsprechend einfach nur 
.
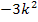Schwieriger ist es dagegen, den zweiten Faktor 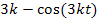nach k abzuleiten. Der Ausdruck 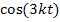stellt nämlich eine verkettete Funktion dar und muss mit der Kettenregel abgeleitet werden. Du darfst also das Nachdifferenzieren mit der Ableitung von 3kt, also das anschließende Multiplizieren mit 3t, nicht vergessen! Die Ableitung von 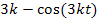nach k lautet deshalb: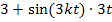 
Nun kannst du bestimmt alleine die gesuchte Ableitung bilden. Bilde sie erst alleine, bevor du weiterliest.
