Kombinationen der verschiedenen Ableitungsregeln

Der Ausdruck 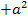enthält ja die Variable x nicht. Also bloßnicht denken, dass die Ableitung von 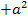hier + 2a ist. Das wäre falsch! 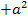ergibt nach x abgeleitet  nämlich + 0 und fällt somit weg.

Jetzt bekommst du es bestimmt alleine heraus, was 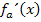ist. Gleich ´mal alleine versuchen und erst nachher mit der restlichen Lösung vergleichen!

Hoffentlich hast du inzwischen selbst die Ableitung 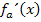ermittelt. Dann kannst du jetzt die korrekte Lösung mit deiner eigenen Lösung vergleichen:

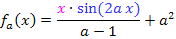
Produktregel (wird nur auf den Zähler z von 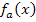angewendet):

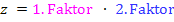
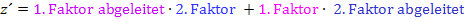
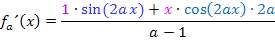
Wirklich vereinfachen lässt sich dabei nichts. Die gesuchte Ableitung lautet:

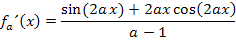
Zu 9b.)

Hier noch einmal die Angabe:

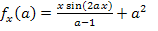mit x ℝ;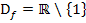 

Die Variable ist in diesem Fall ungewöhnlicher Weise a und der Parameter heißt x. Das heißt, dass du dir x als konkrete Zahl vorstellen musst. Wir leiten jetzt also nach a ab und nicht wie normalerweise nach x. Weil die Variable a im Nenner des Bruchs vorkommt, brauchen wir die Quotientenregel, um den Bruch abzuleiten. Um den Zähler des Bruchs abzuleiten brauchen wir die Produktregel nicht, denn der Zähler ist zwar ein Produkt, doch nur ein Faktor enthält die Variable a. Das x bei 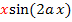ist hier nur eine multiplikative Konstante und wird beim Ableiten nach a einfach abgeschrieben. Allerdings muss die Kettenregel angewendet werden, um den Ausdruck 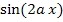nach a abzuleiten.

Terme, die addiert werden, dürfen getrennt abgeleitet und nachher einfach wieder addiert werden. Hier bedeutet das, dass wir jeweils einzeln den Bruch (mit der Quotientenregel und der Kettenregel) und den Ausdruck 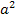ableiten und die Ergebnisse nachher addieren dürfen. 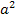nach a abgeleitet ergibt 2a. Das wird dann einfach zur Ableitung des Bruchs dazu gezählt.

Konzentriere dich hier beim Ableiten nur auf das a, nicht auf das x! Hier ist ja a die Variable und nicht x.

Jetzt solltest du alleine versuchen, die Funktion abzuleiten. Erst danach weiterlesen und dein Ergebnis mit der restlichen Lösung vergleichen!

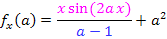
Quotientenregel (wird nur auf den Bruch b angewendet):

Wir fassen im Zähler noch soweit möglich zusammen. Das ergibt:

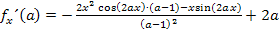
Im Zähler kann außerdem noch x ausgeklammert werden:

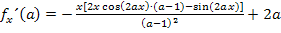
Das x muss aber nicht unbedingt ausgeklammert werden. Du hättest also auch schon vorher einen Schritt vorher aufhören können. Rein theoretisch könnte man außerdem noch alles auf einen gemeinsamen Bruchstrich schreiben. Dazu müsste man alles auf den gemeinsamen Nenner 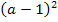bringen, also entsprechend bei 2a mit 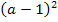erweitern. Doch das macht die Ableitung auch nicht wirklich einfacher. Wir schenken uns daher diesen letzten Schritt. Es geht bei dieser Aufgabe nämlich sowieso hauptsächlich darum, dass du lernst den richtigen Ansatz für die Ableitung zu finden, und weniger um die Vereinfachung.

---