Kombinationen der verschiedenen Ableitungsregeln

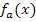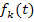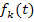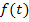Eine Funktion muss man also nach x ableiten. Den Buchstaben a musst du dir dabei einfach als konkrete, feste Zahl denken. Entsprechend muss nach t abgeleitet werden und nicht nach k. Du konzentrierst dich also nur auf t beim Ableiten und denkst dir den Parameter k als feste Zahl. Anders gesagt:Bei oder entspricht das t dem x bei .

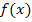In der folgenden Beispielaufgabe geht es genau um diese Problematik. Du musst dabei genau aufpassen, nach welchem Buchstaben abgeleitet werden soll, also welcher Buchstabe die Variable darstellt. Nur wenn bei einem Produkt die Variable wirklich in beiden Faktoren vorkommt, brauchst du die Produktregel. Bei Quotienten gilt entsprechend, dass die Quotientenregel wirklich nur dann angewendet wird, wenn im Nenner (unterhalb des Bruchstrichs) die Variable vorkommt.

Steht im Nenner dagegen ausschließlich eine Zahl oder ein Parameter, wird die Quotientenregel nicht angewendet! Zahlen, mit denen multipliziert wird oder durch die dividiert wird, bleiben beim Ableiten einfach stehen;nur der Rest wird abgeleitet. Steht also im Nenner eines Bruchs keine Variable, wird der Nenner beim Ableiten einfach abgeschrieben und nur der Zähler abgeleitet.

Aber Vorsicht:Zahlen ganz ohne Variable, die addiert oder subtrahiert werden, fallen beim Ableiten weg. (Also auch Parameter, die ganz ohne Variable vorkommen und die plus oder minus gerechnet werden).

9. Bsp.:Schwierige Ableitungen von Funktionenscharen

Differenziere!

a.)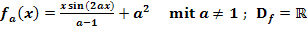

b.) 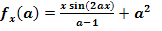mit x ℝ;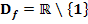

c.)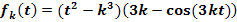

d.)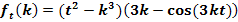

e.)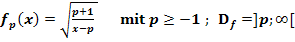

f.)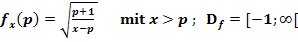

Lösung:

Zu 9a.)

Hier noch einmal die Angabe:

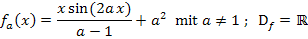
Die Variable ist in diesem Fall x;der Parameter ist hier a. Das heißt:a musst du dir als konkrete Zahl vorstellen. Weil die Variable x im Nenner nicht vorkommt, brauchen wir die Quotientenregel nicht. Der Nenner wird beim Ableiten einfach abgeschrieben – nur der Zähler muss abgeleitet werden. Der Zähler ist allerdings ein Produkt, das die Variable x in beiden Faktoren enthält. Deshalb muss beim Ableiten des Zählers die Produktregel angewendet werden. Um den zweiten Faktor 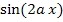abzuleiten, braucht man außerdem die Kettenregel, weil 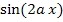eine verkettete Funktion ist. Es ist also mit der Ableitung der inneren Funktion 2ax nachzudifferenzieren, also mit 2a.

Die additive Konstante 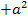, die ganz am Ende der Funktion 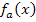steht, fällt beim Ableiten weg. (Additive Konstanten, d.h. Zahlen bzw. Parameter ohne Variable, die addiert oder subtrahiert werden, fallen beim Ableiten immer weg.) 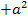ist hier wirklich nur eine additive Konstante, da wir nach x ableiten und nicht nach a.

---