Kombinationen der verschiedenen Ableitungsregeln
Man braucht bei beiden die Kettenregel. Der Sinus bzw. der Kosinus stellen dabei jeweils die äußere Funktion dar, die zuerst abgeleitet werden muss. Die innere Funktion ist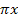 
, sowohl bei 
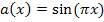als auch bei 
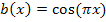. Der Ausdruck 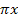bleibt beim Ableiten erst einmal stehen und wird dann nachdifferenziert. Nachdifferenzieren bedeutet hier, dass wir jeweils noch mit der Ableitung von 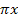, also mit 
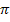, multiplizieren müssen.
Wir beginnen mit 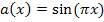. Die äußere Funktion, also der Sinus, ergibt abgeleitet bekanntlich Kosinus. Die innere Funktion 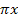bleibt dabei stehen. Dann multiplizieren wir mit der Ableitung der inneren Funktion, also mit 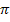. So ergibt sich:
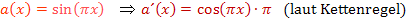
Nun zur Ableitung von 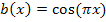. Das funktioniert nach dem gleichen Prinzip. Die äußere Funktion, also der Kosinus, ergibt abgeleitet bekanntlich Minus Sinus. Die innere Funktion 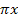bleibt dabei stehen. Dann multiplizieren wir mit der Ableitung der inneren Funktion, also mit 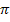. So ergibt sich:
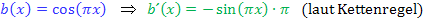
Nebenrechnung zur Ermittlung der Nennerableitung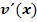 
:
Nenner: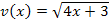 
Um die Nennerableitung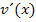 
zu bilden, brauchen wir wieder die Kettenregel. Die Wurzel stellt die äußere Funktion dar. 
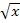ergibt abgeleitet 
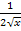. Weil statt x jetzt aber die innere Funktion 
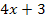unter der Wurzel steht, muss mit der Ableitung von 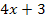, also mit 4 nachdifferenziert werden. So ergibt sich:
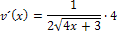
Wir stellen unsere Zwischenergebnisse noch übersichtlich zusammen.
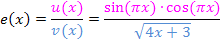
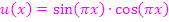
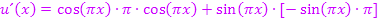
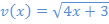
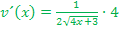
Wir setzen in die Formel der Quotientenregel ein.
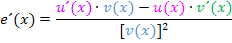
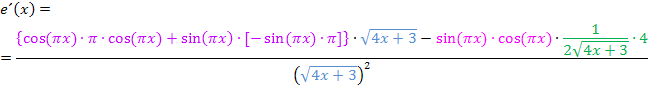
Hoffentlich kannst du jetzt nachvollziehen, wie die Ableitung gebildet wurde. Wenn es dir jetzt reicht, kannst du es nun gut sein lassen und auf die weitere Vereinfachung der Ableitung verzichten. Noch schwerere Ableitungen wirst du in der Schule sicher nicht berechnen müssen.
Für den interessierten Schüler hier noch alle weiteren Schritte zur Vereinfachung der Ableitung.
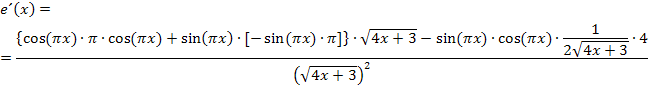
Zuerst fassen wir die Ausdrücke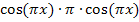 
und 
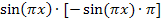jeweils zusammen zu 
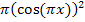bzw.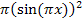 
. Im hinteren Teil des Zählers, also hinter dem Minuszeichen kürzen wir den kleinen Bruch mit 2 und schreiben außerdem 
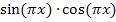in den Zähler des Bruchs. Im Nenner des gesamten Bruchs heben sich Wurzel und Quadrat gegenseitig weg.
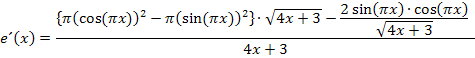
Nun wollen wir im Zähler einen kompletten Bruch erzeugen, d.h. wir bringen alles, was im Zähler des gesamten Bruchs steht, auf einen gemeinsamen Nenner. Der Hauptnenner des Zählers ist logischerweise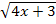 
. Den Ausdruck vor dem Minus im Zähler müssen wir daher mit 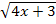erweitern.
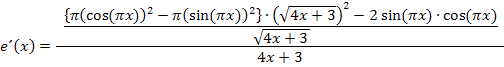
Wurzel und Quadrat heben sich bei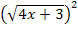 
gegenseitig weg.
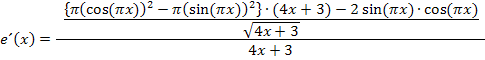
Nun wollen wir den Doppelbruch beseitigen.
