Kombinationen der verschiedenen Ableitungsregeln
Die gegebene Funktion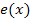 
ist wirklich sehr heftig. Es liegt hier ein Bruch mit x im Nenner vor, so dass die Quotientenregel angewendet werden muss. Es gilt:
Zähler abgeleitet mal Nenner minus Zähler mal Nenner abgeleitet und das Ganze geteilt durch den Nenner zum Quadrat.
Um aber den Zähler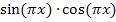 
abzuleiten, benötigt man die Produktregel, weil es sich dabei um ein Produkt handelt, das in beiden Faktoren x enthält. Leider muss man auch noch jeweils die Kettenregel anwenden, um die einzelnen Faktoren des Produkts abzuleiten, da die einzelnen Faktoren selbst verkettete Funktionen darstellen.
Um den Nenner der Funktion 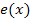abzuleiten, muss wiederum die Kettenregel angewendet werden. Wir haben also einiges zu tun. Versuche doch alleine zumindest den Ansatz der Ableitung 
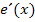zu bilden! Vereinfachen musst du ihn nicht vollständig.
Zu deiner Kontrolle:
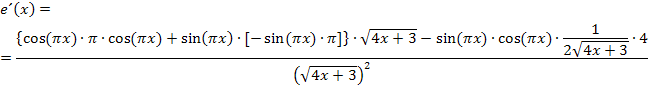
Wenn du alleine auf diesen Ansatz gekommen bist, kannst du echt stolz sein. Das war eine Superleistung! Wenn du nicht selbst darauf gekommen bist, bitte nicht den Kopf hängen lassen. Diese Aufgabe ist wirklich extrem schwer. Versuche dann an Hand der folgenden Erklärung die einzelnen Schritte beim Ableiten von 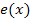nachzuvollziehen.
Ausführliche Erklärung:
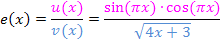
Zählerfunktion: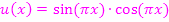 
Nennerfunktion: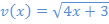 
Laut Quotientenregel gilt:
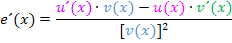
Dafür benötigen wir noch die Zählerableitung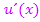 
und die Nennerableitung 
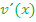. Weil sich hier beide nicht so leicht ermitteln lassen, machen wir das jeweils in einer Nebenrechnung und setzen die Ergebnisse erst später in die Formel der Quotientenregel ein.
Nebenrechnung zur Ermittlung der Zählerableitung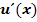 
:
Zählerfunktion: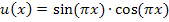 
Die Funktion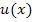 
ist ein Produkt, das in beiden Faktoren x enthält. Wir benötigen zum Ableiten daher die Produktregel:
Ersten Faktor ableiten mal zweiten hinschreiben plus ersten Faktor hinschreiben mal zweiten Faktor ableiten.
Wir verwenden hier ausnahmsweise die Bezeichnungen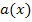 
für den ersten Faktor des Produkts 
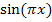und 
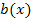für den zweiten Faktor 
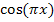. (Die Benennungen 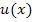und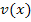 
sind schließlich schon für den kompletten Zähler bzw. für den Nenner der Funktion 
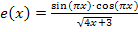vergeben.)
Zählerfunktion: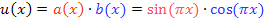 
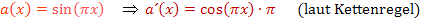
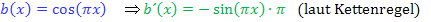
Einsetzen in die Formel der Produktregel:
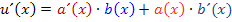
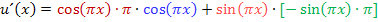
Du hast nicht verstanden, wie man auf die Ableitungen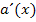 
und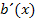 
der Einzelfaktoren 
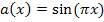und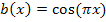 
kommt? Ok, dann noch einmal ganz langsam.
