Kombinationen der verschiedenen Ableitungsregeln
Wir schreiben den Ausdruck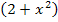 
in den Zähler des kleinen Bruchs.
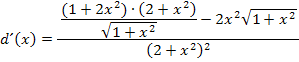
Nun werden die Klammern im Zähler des kleinen Bruchs ausmultipliziert und danach soweit möglich zusammengefasst.
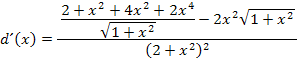
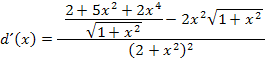
Nun bringen wir den gesamten Zähler auf einen gemeinsamen Bruchstrich. Der Hauptnenner ist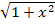 
. Den Ausdruck hinter dem Minus-Zeichen muss man dabei mit 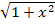erweitern.
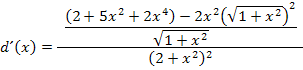
Wurzel und Quadrat heben sich bei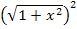 
gegenseitig auf. Nur die Klammer brauchen wir noch, da eine Wurzel wie eine Klammer wirkt.
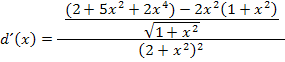
Wir multiplizieren aus, um die hintere Klammer aufzulösen. Die vordere runde Klammer kann einfach weggelassen werden;sie ist unnötig, weil kein Minus oder Mal davor steht. (Sie diente nur der besseren Übersicht.)
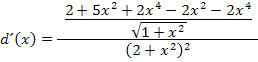
Zusammengefasst ergibt sich:
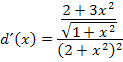
Nun wollen wir den Doppelbruch beseitigen. Dabei stellen wir uns den Nenner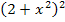 
als Bruch mit dem Nenner 1 vor.
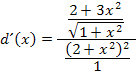
Der längste Bruchstrich ist der sogenannte Hauptbruchstrich. Statt des Hauptbruchstrichs schreiben wir ein Geteilt-Zeichen.
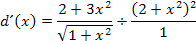
Bekanntlich wird durch einen Bruch dividiert, indem man mit dem Kehrwert multipliziert.
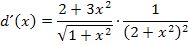
Schreibt man alles auf einen gemeinsamen Bruchstrich, ergibt sich mit vertauschter Reihenfolge der Faktoren im Nenner:
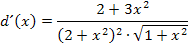
Der Nenner von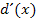 
ist noch nicht rational, d.h. noch nicht ohne Wurzel geschrieben. Man könnte den Nenner rational machen, indem man mit 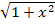erweitert, d.h. im Zähler und Nenner damit multipliziert. Doch würde 
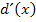dadurch nicht wirklich vereinfacht. Daher verzichten wir darauf. Wir sind also fertig!
Diese Ableitung war nicht nur schwierig zu bilden, sondern auch extrem aufwendig zu vereinfachen. Du kannst diese Aufgabe jedoch als Extremfall auffassen, der wahrscheinlich in vergleichbarem Schwierigkeitsgrad nicht in Prüfungen verlangt wird. Die Vereinfachung dauert einfach viel zu lange. Wenn überhaupt, wird daher sicher nur der Ansatz der Ableitung verlangt, jedoch nicht die vollständige Vereinfachung. Die komplette Vereinfachung wurde hier nur gezeigt, damit du es dir einmal ansehen konntest, wie man auch so eine riesige Ableitung zusammenfasst. Am Endergebnis erkennt man übrigens sofort, dass die Funktion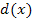 
streng monoton steigend ist, also keine Extrema besitzt, weil die Ableitung 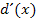immer positiv ist. (Sowohl der Zähler 
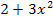ist immer positiv, als auch die beiden einzelnen Faktoren im Nenner und somit der gesamte Nenner 
.)
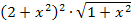Zu 8e.)
Hier noch einmal die Funktion, die abgeleitet werden soll: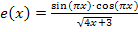 
Diese Funktion ist noch schwieriger abzuleiten als die im vorherigen Beispiel.
