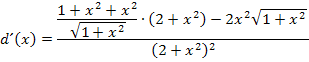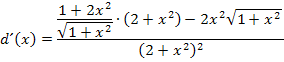Kombinationen der verschiedenen Ableitungsregeln
Laut Produktregel gilt: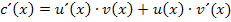 
Dass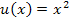 
abgeleitet 
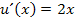ergibt, dürfte dir klar sein. Um aber 
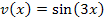abzuleiten, benötigt man die Kettenregel:Äußere Funktion, hier den Sinus, ableiten, dabei innere Funktion 
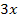stehen lassen und mit der Ableitung der inneren Funktion, also hier mit der Zahl 3, multiplizieren. Du darfst daher keinesfalls das Nachdifferenzieren mit der Zahl 3 vergessen!
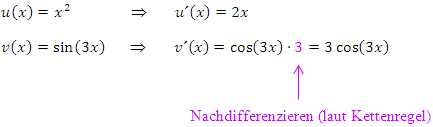
Nun kannst du bestimmt die Ableitung von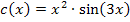 
berechnen. Probiere es doch gleich!
Du solltest das folgende Ergebnis erhalten:
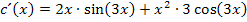
Wirklich vereinfachen lässt sich hier nicht viel. Wir schreiben einfach:
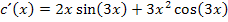
Nur das x könnte noch ausgeklammert werden.
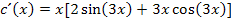
Weiter lässt sich diese Ableitung nicht vereinfachen.
Zu 8d.)
Hier noch einmal die Angabe: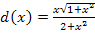 
So, jetzt wird es schwierig. Insgesamt liegt ein Quotient mit x im Nenner vor, so dass man beim Ableiten der Funktion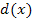 
die Quotientenregel verwenden muss. Um die Ableitung des Zählers 
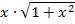zu bilden, braucht man aber auch die Produktregel, weil es sich beim Zähler um ein Produkt handelt, das in beiden Faktoren x enthält. Um den zweiten Faktor des Produkts 
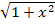abzuleiten, muss aber zusätzlich die Kettenregel angewendet werden. Die Wurzel stellt dabei die äußere Funktion dar, 
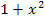dagegen die innere Funktion. Die innere Funktion 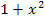wird beim Ableiten von 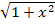bei der Ableitung der Wurzel an Stelle von x hingeschrieben und dann erst nachdifferenziert.
Versuche dich doch gleich ´mal selbst an dieser zugegeben echt schwierigen Funktion! Wenn du diese Funktion korrekt ableiten kannst, dann darfst du davon ausgehen, dass du so ziemlich jede Funktion ableiten kannst. Ob du die Ableitung noch vereinfachen willst, bleibt dir selbst überlassen. Es ist sehr aufwendig. Es reicht also im Prinzip, wenn du den Ansatz für die Ableitung bildest, aber nicht mehr weiter vereinfachst. Zu deiner Kontrolle folgt natürlich der komplette Lösungsweg.
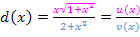
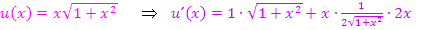
Du kannst nicht nachvollziehen, wie man auf u´(x) kommt? Dan gehe zu:Ausführliche Erklärung zu u´(x) Bsp. 7d.)
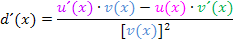
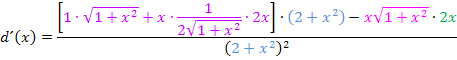
Jetzt wird die Ableitung noch vereinfacht.
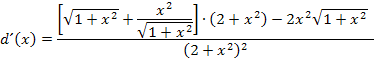
Wir schreiben die Ausdrücke in der eckigen Klammer auf einen gemeinsamen Bruchstrich. Dazu muss natürlich alles innerhalb der eckigen Klammer auf den Hauptnenner 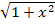gebracht werden, d.h. wir müssen bei dem ersten Summanden 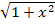mit dem Hauptnenner, der hier zufälligerweise ebenfalls 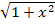ist, erweitern. Das kann man dann natürlich mit einem Quadrat schreiben.
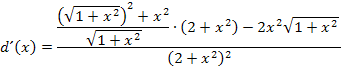
Wurzel und Quadrat heben sich bei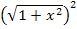 
gegenseitig auf.
