Kombinationen der verschiedenen Ableitungsregeln
Laut Kettenregel muss zuerst die äußere Funktion, hier also die e-Funktion, abgeleitet werden. Es gilt: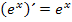 
Dabei bleibt der Bruch erst einmal statt x bei der Ableitung der äußeren Funktion stehen und wird gleich im Anschluss nachdifferenziert. Weil der Bruch aber ein x im Nenner enthält, muss beim Ableiten des Bruchs, d.h. beim Nachdifferenzieren, die Quotientenregel angewendet werden.
Die Zahl 0,5 stört uns beim Ableiten von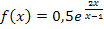 
nicht. Es handelt sich bei der Zahl 0,5 um eine multiplikative Konstante, also um eine Zahl ohne x, mit der multipliziert wird. Solche Zahlen werden beim Ableiten einfach abgeschrieben;nur der Rest wird abgeleitet.
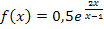
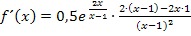
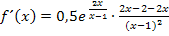
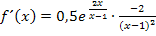
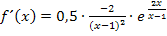
Mit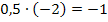 
ergibt sich:
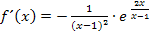
Man könnte den Ausdruck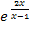 
auch in den Zähler des vorderen Bruchs schreiben, doch das sieht nicht wirklich schöner aus. Sonst kann man nichts mehr machen. Wir lassen 
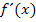wie es jetzt ist.
Zu 10f.)
Hier noch einmal die Angabe: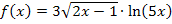 
Bei dieser Funktion handelt es sich offensichtlich um ein Produkt, das in beiden Faktoren die Variable x enthält, das sich aber auch nicht ausmultiplizieren lässt. Wir brauchen deshalb zum Ableiten von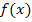 
die Produktregel. Leider sind beide Faktoren des Produkts verkettete Funktionen, so dass man beim Ableiten der einzelnen Faktoren jedes Mal die Kettenregel anwenden muss. Zur Erinnerung: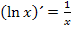 
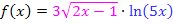
Produktregel:
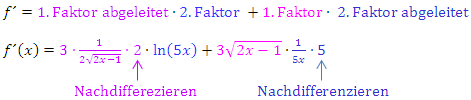
Vereinfachen von :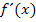
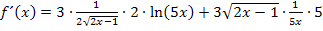
Beim vorderen Term mit 2 kürzen und beim hinteren Term mit 5 ergibt:
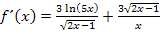
Jeweils erweitern, um alles auf den gleichen Nenner zu bringen:
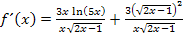
Wurzel und Quadrat heben sich im Zähler des zweiten Bruchs auf.
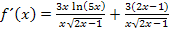
Auf einen gemeinsamen Bruchstrich geschrieben:
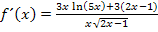
Im Zähler lässt sich nun die Zahl 3 komplett ausklammern. (Deshalb wurde vorher die 3 auch nicht in die hintere Klammer hinein multipliziert.)
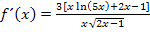
Man kann die Zahl 3 auch vor den Bruch hinschreiben.
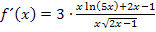
Der Nenner der Ableitung enthält noch eine Wurzel, d.h. er ist noch nicht rational. (Normalerweise formt man immer so lange um, bis keine Wurzel mehr im Nenner steht.) Um den Nenner hier rational zu machen, müsste man mit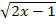 
erweitern, also mit 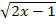im Zähler und Nenner multiplizieren. Dadurch würde dann die Wurzel im Nenner wegfallen, doch wirklich schöner sieht das dann auch nicht aus, weil der Zähler so kompliziert werden würde. Wir verzichten daher ausnahmsweise auf das Rationalmachen des Nenners und lassen es hiermit gut sein.
