Kombinationen der verschiedenen Ableitungsregeln

Zu 10c.)

Hier noch einmal die Angabe: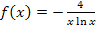

Bei dieser Funktion handelt es sich um einen Quotienten, so dass wir die Quotientenregel zum Ableiten von 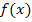brauchen. Der Nenner ist dabei allerdings ein Produkt, so dass wir außerdem die Produktregel anwenden müssen, um die Ableitung des Nenners zu bilden. Das Minus vor dem Bruchstrich lassen wir einfach vor dem Bruch stehen. Bei der Ableitung steht es dann auch wieder vor dem Bruch. (Stattdessen könntest du das Minus aber auch in den Zähler der Funktion schreiben, wenn dir das lieber ist.)

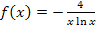
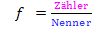
Quotientenregel:

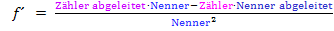
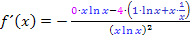
Vereinfachung von :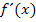

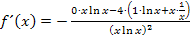
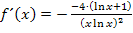
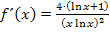
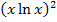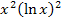Man könnte theoretisch noch die Zahl 4 im Zähler in die Klammer hinein multiplizieren, doch würde das keine wirkliche Vereinfachung mit sich bringen. Wir verzichten deshalb darauf. Des Weiteren könnte man im Nenner statt auch schreiben, doch auch dies ist nicht wirklich sinnvoll. Daher lassen wir die Ableitung so stehen, wie sie jetzt ist. Fertig!

Zu 10d.)

Hier noch einmal die Angabe: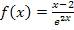

Es handelt sich bei dieser Funktion um einen Bruch mit x im Nenner. Daher brauchen wir zum Ableiten wieder die Quotientenregel. Der Nenner ist allerdings eine verkettete Funktion, so dass wir zum Ableiten des Nenners auch noch die Kettenregel brauchen. Bei 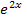bildet die e-Funktion die äußere Funktion und 2x die Innere. Laut Kettenregel muss man zuerst die äußere Funktion ableiten, dabei die Innere stehen lassen und dann noch mit der Ableitung der Inneren multiplizieren / nachdifferenzieren. Die Ableitung von ist bekanntlich , daher ergibt 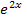abgeleitet 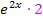. (Die 2 kommt vom Nachdifferenzieren;2x ergibt abgeleitet bekanntlich 2.) Es gilt somit:  .

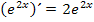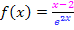
Quotientenregel:

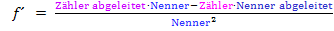
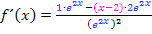
Vereinfachung der Ableitung:

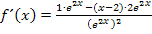
Wir klammern im Zähler den Faktor 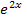aus:

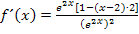
Nun liegt im Zähler ein Produkt vor, so dass man kürzen darf. Wir kürzen mit :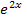

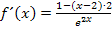
Ausmultiplizieren und Zusammenfassen im Zähler ergibt:

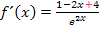
Beachte das Pluszeichen vor der Zahl 4!

Dieses Plus ergibt sich, weil sich bei 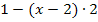das Minus vor der Klammer auf den gesamten nachfolgenden Ausdruck bezieht. Das Minus dreht also praktisch die nachfolgenden Vorzeichen alle um: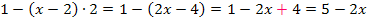

Die gesuchte Ableitung lautet:

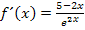
Zu 10e.)

Hier noch einmal die Angabe: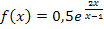

Bei der vorliegenden Funktion steht der Bruch im Exponenten, die Zahl e bildet die Basis. Es handelt sich daher um eine verkettete Funktion, wobei 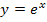die äußere Funktion ist und der Bruch die Innere.

---