Kombinationen der verschiedenen Ableitungsregeln

Dir ist der Schritt mit dem Ausklammern von 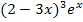nicht klar? Ok, dann diesen Schritt noch einmal ganz ausführlich:

Wir haben für die Ableitung erhalten:

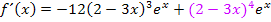
Statt 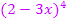kann man sich auch 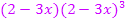denken:

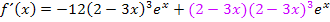
Jetzt siehst du bestimmt, dass die Faktoren 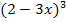und jeweils beide sowohl vor dem Pluszeichen als auch danach vorkommen.

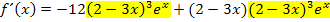
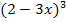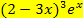Deshalb kann man die Faktoren und , d.h. den Ausdruck , insgesamt ausklammern:

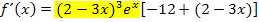
Jetzt ist hoffentlich alles klar. Es ist sehr wichtig, dass du den Schritt mit dem Ausklammern wirklich verstanden hast. Bei vielen anderen Ableitungen wird ähnlich vorgegangen, ganz besonders bei Ableitungen mit oder ähnlichem. Merke dir dieses Vorgehen beim Vereinfachen der Ableitung!

Tipp:Grundsätzlich bei 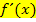alles ausklammern, was geht.

Dadurch erhält man die Ableitung letztendlich als Produkt, also in einer Form, in der sie sich leicht gleich Null setzen lässt. Das ist besonders für die Berechnung der Extrema von 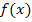wichtig.

Zu 10b.)

Hier noch einmal die Angabe: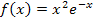

Auch bei dieser Funktion braucht man zum Ableiten wieder Produkt und Kettenregel, allerdings wird die Kettenregel nun beim Ableiten des zweiten Faktors des Produkts benötigt, also beim Ableiten von 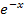. Ist dir klar, warum du dabei die Kettenregel brauchst? 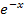ist schließlich eine verkettete Funktion mit als äußerer Funktion und – x als innerer Funktion. Daher darfst du beim Ableiten von 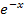keinesfalls das Nachdifferenzieren mit der Zahl -1 vergessen. (-1 ist ja die Ableitung von – x.)

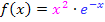
Produktregel:

Vereinfachung von :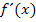

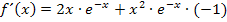
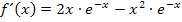
Ausklammern von 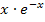ergibt:

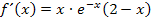
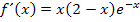
Das x multiplizieren wir nicht in die Klammer hinein, denn in der vorliegenden Form lässt sich die Ableitung besser gleich Null setzen als in der ausmultiplizierten Form. Bei der Berechnung der Extrema müsste man bekanntlich die Gleichung 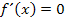lösen. In der vorliegenden Form von 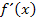lässt sich direkt ablesen, dass nur fü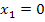r oder 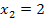die Ableitung Null wird. Ein Produkt ist schließlich genau dann gleich Null, wenn einer der Faktoren Null ergibt. Für welche x gilt dann 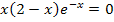? Der erste Faktor x wird Null für x = 0;der zweite Faktor 2 – x ergibt Null für x = 2. Der dritte Faktor 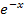wird niemals Null, denn 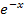ist immer positiv. Wir multiplizieren 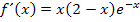also nicht weiter aus. Fertig!

Hinweis:Nur wenn man auch noch die zweite Ableitung bilden müsste, wäre es sinnvoll, x in die Klammer hinein zu multiplizieren. Danach läge 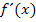nämlich als Produkt vor, das nur noch in zwei Faktoren x enthält und nicht in drei;dann könnte mit der Produktregel ein zweites Mal abgeleitet werden. Die Produktregel kann schließlich nur auf Produkte angewendet werden, welche in genau zwei Faktoren die Variable enthalten, aber eben nicht in drei oder mehr.

---