Kombinationen der verschiedenen Ableitungsregeln

Wenn du aber doch sehen willst, was man noch so alles machen könnte, hier die weiteren Schritte:

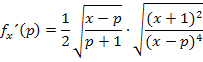
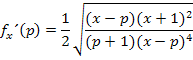
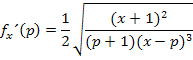
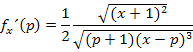
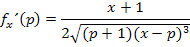
Teilweise radizieren ergibt:

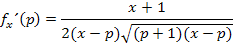
Nenner rational machen durch Erweitern mit 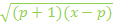liefert:

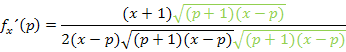
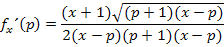
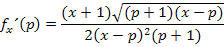
Mehr lässt sich definitiv nicht machen. Damit ist diese Aufgabe wirklich gelöst.

Alle nachfolgenden Beispielaufgaben sind nur für Schüler geeignet, die im Unterricht bereits die e- und ln-Funktion gelernt haben. Für alle anderen Schüler ist hier Schluss. Weitere Beispiele für schwierigere Ableitungen und ihre Anwendung findest du auch bei Berechnung der Extrema mit Hilfe der Monotonie.

10. Bsp.:Schwierige Ableitungen mit Exponential- und Logarithmusfunktionen

Bilde jeweils die Ableitung 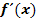der Funktion 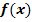und vereinfache 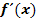anschließend soweit möglich!

a.)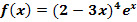

b.)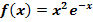

c.)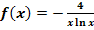

d.)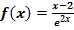

e.)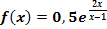

f.)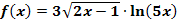

Lösung:

Zu 10a.)

Hier noch einmal die Angabe: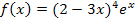

Um diese Funktion abzuleiten, braucht man zuerst die Produktregel und dabei beim Ableiten des ersten Faktors zusätzlich die Kettenregel. Die abzuleitende Funktion ist schließlich ein Produkt, das in beiden Faktoren die Variable x enthält;daher muss beim Ableiten von 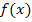die Produktregel angewendet werden. Der erste Faktor des Produkts ist allerdings eine verkettete Funktion;deshalb muss beim Ableiten des ersten Faktors die Kettenregel angewendet werden.

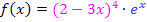
Produktregel:

Erläuterungen zur Ableitung des ersten Faktors:

Der erste Faktor 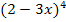wurde mit der Kettenregel abgeleitet. Diese besagt:Abgeleitet wird zu Beginn nur die äußere Funktion, hier also 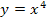. Bei der Ableitung der äußeren Funktion 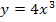wird an Stelle von x die innere Funktion 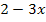hingeschrieben;die innere Funktion wird also nicht gleichzeitig mit der äußeren Funktion abgeleitet, sondern erst mal abgeschrieben und anschließend nachdifferenziert. Anders formuliert:Beim Ableiten von 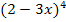bleibt die innere Funktion 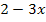zuerst stehen und wird nachher abgeleitet / nachdifferenziert. D.h. es muss noch mit der Ableitung der inneren Funktion, hier mit -3, multipliziert werden.

Die Ableitung 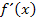soll noch vereinfacht werden. Wichtig ist hierbei vor allem das Ausklammern von .

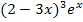Vereinfachung von :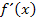

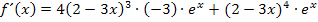
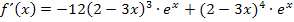
Ausklammern von 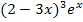ergibt:

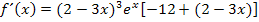
Die runde Klammer innerhalb der eckigen Klammer ist eigentlich unnötig. Sie wurde nur gesetzt, damit du den Schritt des Ausklammerns besser nachvollziehen konntest. Ab sofort lassen wir diese runde Klammer aber wieder weg.

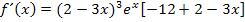
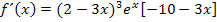
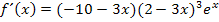
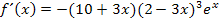
So lassen wir die Ableitung jetzt stehen. Fertig!

---