Kombinationen der verschiedenen Ableitungsregeln
Zu deiner Kontrolle, hier der Rest der Lösung:
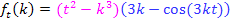
Produktregel:
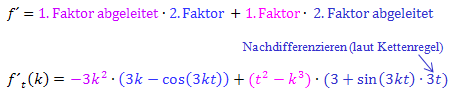
Vereinfachen lässt sich hier nicht mehr viel. Man könnte zwar aus dem zweiten Faktor die Zahl 3 ausklammern, aber das bringt auch nicht wirklich viel. Also sparen wir uns das.
Zu 9e.)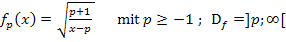 
Die Variable ist hier ganz normal mit x bezeichnet;der Parameter ist p. Es soll also ganz normal nach x abgeleitet werden. Das macht die ganze Sache zumindest etwas einfacher. Man braucht zum Ableiten von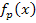 
die Kettenregel, weil 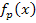eine verkettete Funktion ist. Dabei stellt die Wurzel die äußere Funktion und der Bruch die innere Funktion dar. Laut Kettenregel wird zuerst nur die äußere Funktion, d.h. hier die Wurzel, abgeleitet. Dabei bleibt die innere Funktion (also der Bruch) noch stehen und wird erst direkt anschließend nachdifferenziert. Um die Ableitung des Bruchs zu bilden, muss die Quotientenregel angewendet werden, weil im Nenner des Bruchs die Variable x vorkommt. Dass im Zähler kein x steht, ist dafür irrelevant. Trotzdem wird zum Ableiten des Bruchs die Quotientenregel benützt. Aber zuerst muss man natürlich laut Kettenregel die äußere Funktion 
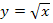ableiten. (Erst beim Nachdifferenzieren, also beim nachfolgenden Ableiten des Bruchs, braucht man dann zusätzlich zur Kettenregel die Quotientenregel.) Weißt du noch, wie man 
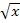nach x ableitet? Zur Erinnerung: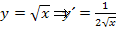 
(Siehe auch:Nähere Erläuterungen zur Ableitung der Wurzel)
Jetzt müsstest du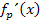 
eigentlich wirklich alleine ermitteln können, zumindest ´mal den Ansatz. Nur noch ein kleiner Tipp vorweg:Der Zähler des Bruchs enthält kein x, deshalb ist die Ableitung des Zählers einfach 0. Der Zähler p + 1 entspricht ja quasi einer gewöhnlichen Zahl und eine Zahl ganz ohne Variable ergibt abgeleitet immer 0. Diese Null darfst du nicht einfach weglassen bei der Quotientenregel. So, los geht´s! Spätestens jetzt 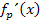selbständig bilden und erst nachher weiterlesen!
Du hast inzwischen hoffentlich selbst versucht die Ableitung zu bilden. Zur Kontrolle hier die komplette Rechnung:
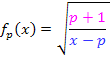
Quotientenregel (nur zum Nachdifferenzieren des Bruchs b):
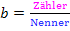
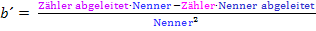
Hier die Ableitung der gesamten Funktion laut Kettenregel:
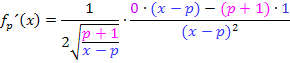
Wir vereinfachen die Ableitung noch.
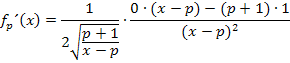
Den Ausdruck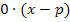 
können wir natürlich weg lassen. (Hättest du übrigens die 0 nicht hingeschrieben, wäre fälschlicherweise 
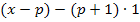im Zähler stehengeblieben. Deshalb darf man die Null nicht vergessen.)
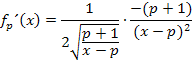
Man teilt durch einen Bruch, indem man mit dem Kehrwert multipliziert.
