Die Quotientenregel
Vermutlich würdest du dazu die Klammern im Zähler auflösen, indem du jeweils ausmultiplizierst. Das ist natürlich nicht falsch, doch geht es auch geschickter. Im Zähler steht momentan eine Differenz. Sowohl im Minuend (Ausdruck vor dem Minus) als auch im Subtrahend (Ausdruck hinter dem Minus) kommt 
vor. Daher kann im Zähler ausgeklammert werden. Man kann auch gleich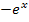 
ausklammern. Ob du lieber oder 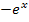ausklammerst, musst du selbst entscheiden. Pass auf jeden Fall sehr gut bei den Vorzeichen auf! Wir werden im Folgenden 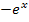ausklammern.
Hier noch einmal die noch nicht vereinfachte Ableitung:
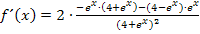
Wir vertauschen die Reihenfolge der Faktoren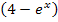 
und , damit du besser erkennen kannst, dass sich 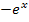ausklammern lässt.
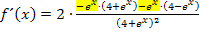
Jetzt klammern wir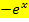 
aus. Damit du besser erkennen kannst, welche Klammer durch das Ausklammern neu entsteht, verwenden wir dafür eine eckige Klammer. (Nach dem Ausklammern sind in diesem Fall die runden Klammern nicht mehr nötig;sie werden nur zur Verdeutlichung im ersten Schritt gesetzt. Du kannst sie in diesem Beispiel auch völlig weglassen. Aber Vorsicht:Das ist nicht bei allen Aufgaben der Fall.)
Ausklammern von 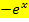im Zähler und nachfolgendes Zusammenfassen in der eckigen Klammer ergibt:
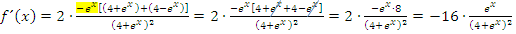
Du kannst die -16 natürlich auch in den Zähler schreiben.
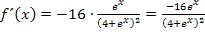
So sieht die Ableitung doch ganz gut aus. Wir sind fertig.
Anmerkung:
Man erkennt an der Ableitung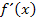 
direkt, dass die Funktion 
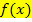streng monoton fallend ist, weil die Ableitung immer negativ ist. Nicht klar? Betrachten wir ´mal die Ableitung in der Form 
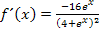genauer. Der Nenner ist wegen des Quadrats (gerade Potenz!) immer positiv, egal was man für x einsetzt. Der Zähler ist hier grundsätzlich negativ, da immer positiv und somit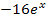 
immer negativ ist. Da Minus durch Plus wieder Minus ergibt, ist 
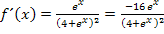für jedes beliebige x negativ: 
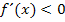Daher muss der Funktionsgraph streng monoton fallend sein. Die Funktion kann somit kein Extremum besitzen.
Zu 4g.) Nur für Schüler, die im Unterricht die Funktion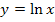 
schon behandelt haben!
Hier noch einmal die Funktionsgleichung: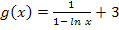 
Es dürfte inzwischen an sich kein großes Problem mehr für dich darstellen, eine Funktion mit Hilfe der Quotientenregel abzuleiten. Bedenke allerdings, dass die Ableitung einer additiven Konstante 0 ist. Normalerweise lässt man die Null natürlich weg, weil man sich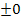 
schließlich schenken kann. So fällt in diesem Beispiel beim Ableiten die Zahl 
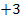, die hinter dem Bruch steht, einfach weg.
