Die Quotientenregel
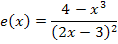
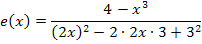
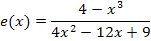
Nun können wir mit Hilfe der Quotientenregel die Ableitung berechnen. Probiere es doch gleich ´mal alleine!
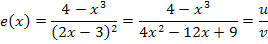
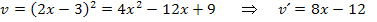
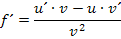
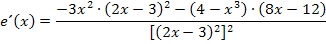
Beachte, dass v nicht in der ausgerechneten Form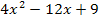 
, sondern in der Form 
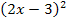für v in die Quotientenregel eingesetzt wird. Die Umformung 
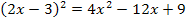wurde nur durchgeführt, damit wir die Ableitung v´bilden konnten. Es ist wichtig, dass du wirklich 
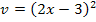in der Quotientenregel für v schreibst, denn sonst kannst du nachher nicht erkennen, dass sich im Zähler der Ableitung der Faktor 
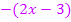ausklammern lässt. Vorher muss allerdings aus der letzten Klammer 
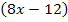die Zahl 4 ausgeklammert werden.
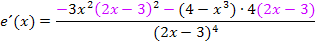
Jetzt multiplizieren wir im Zähler nicht aus, sondern klammern stattdessen im Zähler insgesamt den Faktor 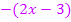aus. Dieser Faktor kommt schließlich sowohl vor dem Minus als auch hinter dem Minus im Zähler vor. Daher kann er aus dem Zähler komplett ausgeklammert werden.
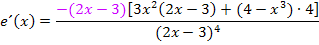
Nun liegt im Zähler insgesamt ein Produkt vor.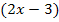 
kommt im Zähler und Nenner vor. Deshalb kann man den Faktor 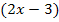jetzt kürzen. Daher haben wir vorher überhaupt ausgeklammert. Im Zähler verschwindet der Faktor durch das Kürzen vollständig, im Nenner erniedrigt sich der Exponent um 1. Wenn du nicht verstehst, warum der Exponent durch das Kürzen um 1 kleiner wird, siehe:Ausführliche Erklärung zum Kürzen von (2x – 3)
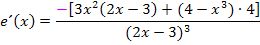
Diesen Trick solltest du dir gut merken! Das Ausklammern und anschließende Kürzen eines Faktors aus dem gesamten Zähler der Quotientenregel, klappt immer, wenn die abzuleitende Funktion einen Nenner der Form Klammer zum Quadrat (oder hoch drei, hoch vier …) hat. Der ausgeklammerte Faktor kann dann immer gekürzt werden. So lässt sich beispielsweise bei der Ableitung der Funktion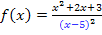 
nachher ganz sicher der Faktor 
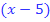im Zähler ausklammern und danach kürzen oder bei der Ableitung der Funktion 
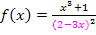der Faktor 
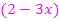. (Zur Übung kannst du das gleich selbst überprüfen. Die Lösungen sind hier jedoch nicht gezeigt.) Eventuell muss man vorher aber etwas aus den Klammern hinter dem Minus der Quotientenregel ausklammern, so wie in diesem Beispiel bei 
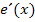die Zahl 4, die wir oben aus 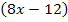ausgeklammert haben.
Jetzt müssen wir bei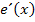 
nur noch in der eckigen Klammer ausmultiplizieren und soweit möglich zusammenfassen.
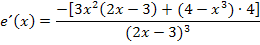
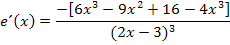
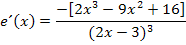
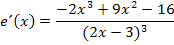
Die Potenz im Nenner rechnen wir nicht aus, da es die Ableitung nur unhandlicher werden ließe. Wir sind also fertig!
Hinweis:Wollte man den Nenner auszurechnen, bräuchte man entweder das Pascalsche Dreieck oder direkt die Formel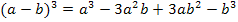 
oder du rechnest 
…
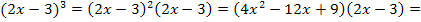Dass dies den Nenner nicht einfacher macht, dürfte hoffentlich einleuchten.
