Die Quotientenregel
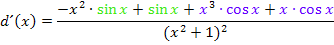
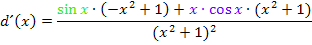
Damit es schöner aussieht, kann noch jeweils die Reihenfolge der Summanden innerhalb der Klammern vertauscht werden. Es ist schließlich nicht so angenehm, wenn ein Minus-Zeichen vorne steht, wie bei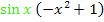 
. Bei den anderen Klammern ist es eigentlich egal, in welcher Reihenfolge die Summanden stehen, weil bei ihnen sowieso kein Minus vorkommt. Wir drehen die Reihenfolge nur deshalb um, weil dann überall die gleiche Reihenfolge, zuerst Zahl dann 
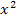, entsteht.
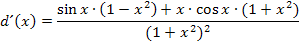
Die letzten beiden Umformungen hätten nicht unbedingt gemacht werden müssen;sie dienen nur der „Kosmetik“. Die Ableitung sieht danach einfach „schöner“ aus. Aber weiter lässt sich die Ableitung nun wirklich nicht mehr vereinfachen. Kürzen darf man hier nämlich nicht! Es handelt sich beim Zähler schließlich um eine Summe und du kennst bestimmt den Spruch „aus Differenzen und Summen kürzen nur die Dummen“. Der Spruch ist zwar irgendwie gemein – wer ist schon dumm, bloßweil er ´mal falsch gekürzt hat, doch darf man bei Differenzen und Summen niemals kürzen. Also hier bloßnicht auf die Idee kommen, den Faktor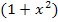 
zu kürzen.
Merke:Bei Ableitungen, die mit der Quotientenregel gebildet wurden, darf niemals gleich gekürzt werden, da eine Differenz (oder Summe) im Zähler der Ableitung steht. Nur wenn sich im Zähler etwas insgesamt ausklammern lässt, darf falls möglich gekürzt werden, weil sich durch das insgesamte Ausklammern im Zähler ein Produkt ergibt. Der Nenner ist wegen der Potenz sowieso auch ein Produkt, so dass er kein Problem beim Kürzen darstellt. Im Beispiel 4e.) kannst du sehen, bei welchen Funktionen das insgesamte Ausklammern eines Faktors im Zähler und nachfolgendes Kürzen dieses Faktors funktioniert. Also gleich zum nächsten Beispiel!
Zu 4e.)
Hier noch einmal die Funktionsgleichung: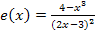 
Die Schwierigkeit bei dieser Funktion ist das Quadrat im Nenner. Dadurch ergeben sich nämlich einige Besonderheiten beim Ableiten. Es handelt sich bei dem Nenner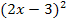 
um einen verketteten, d.h. verschachtelten, Term. Um verkettete Funktionen abzuleiten, verwendet man eigentlich die sogenannte Kettenregel. (Hinweis:Weiter unten werden wir ausführlich besprechen, auf welche Art und Weise Ausdrücke wie z.B. 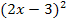mit der Kettenregel direkt abgeleitet werden können, ohne vorher die Klammer auszurechnen. Näheres dazu bei:Die Kettenregel)
Da wir die Kettenregel aber noch nicht eingeführt haben, müssen wir anders behelfen:Wir rechnen einfach das Quadrat im Nenner 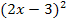mit Hilfe der zweiten Binomischen Formel 
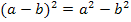aus, bevor wir die Ableitung des Nenners bilden.
