Die Quotientenregel
Dass man beim Ableiten von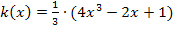 
die Quotientenregel nicht anwendet, dürfte somit klar sein. Es gilt schließlich 
.
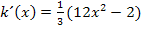Nun wieder zurück zu der gegebenen Funktion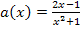 
. Ihr Zähler wird kurz mit u bezeichnet, der Nenner mit v. (Korrekt wäre eigentlich 
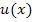für den Zähler und 
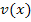für den Nenner, weil sowohl der Zähler als auch der Nenner von x abhängig sind, also x enthalten;doch das ist etwas unhandlich. Daher bleiben wir einfach bei u und v.)
Hier noch einmal die Quotientenregel in Kurzfassung: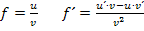 
Damit ergibt sich für die Ableitung von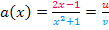 
:
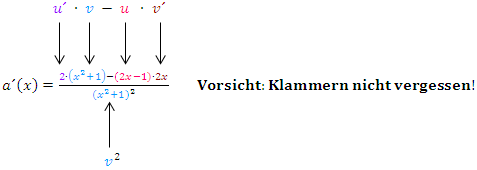
Nun muss die Ableitung aber noch vereinfacht werden. Dazu multiplizieren wir die Klammern im Zähler aus und fassen danach soweit möglich zusammen. Den Nenner könnte man zwar mit der ersten Binomischen Formelebenfalls ausrechnen, doch das würde die Ableitung nicht einfacher, sondern bloßunhandlicher machen. Das Quadrat im Nenner außerhalb der Klammer verrät uns nämlich, dass der Nenner nicht negativ werden kann, was dazu führt, dass man sich bei einer Monotonieuntersuchung keine Gedanken um das Vorzeichen des Nenners machen muss;es reicht den Zähler zu betrachten. Daher solltest du den Nenner nach Anwendung der Quotientenregel immer so lassen, wie er ist und nicht mit einer Binomischen Formel umformen. Rechne doch gleich ´mal alleine weiter!
Vergleiche nun dein Ergebnis mit der nachfolgenden Lösung! Hast du auch wirklich alle Vorzeichen richtig? Vorsicht beim Auflösen der hinteren Klammer;das Minus-Zeichen vor der hinteren Klammer bezieht sich auf alles, was dahinter steht. Deshalb ergibt sich hier letztendlich ein Plus-Zeichen vor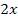 
. (Es ist unten in Rosa geschrieben.)
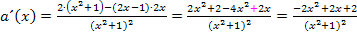
In dieser Form könnte man die Ableitung bereits stehen lassen. Geschickt ist es aber, noch im Zähler die Zahl 2 oder -2 auszuklammern. Ob du lieber 2 oder -2 ausklammerst, kannst du dir selbst aussuchen.
2 ausklammern: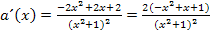 
-2 ausklammern: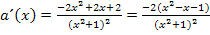 
Weiter lässt sich diese Ableitung nicht vereinfachen. Also sind wir fertig.
Zu 4b.)
Hier noch einmal die Funktionsgleichung: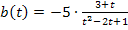 
In diesem Fall ist die Variable nicht x, sondern t. Wir müssen also nach t ableiten, aber das ist kein großes Problem. Das t entspricht praktisch dem x aus den vorherigen Aufgaben. Falls dich die Zahl -5, die vor dem Bruch steht, irritiert, kannst du sie auch einfach mit dem Bruch multiplizieren, d.h. in den Zähler des Bruchs schreiben und dann erst ableiten. An sich ist das aber gar nicht nötig, wenn man weiß, dass Zahlen, die multipliziert werden, beim Ableiten einfach stehen bleiben. (Nur Zahlen mit Plus oder Minus fallen beim Ableiten weg!
