Die Quotientenregel

Dass keine Extrema vorliegen können, erkennt man auch schon daran, dass im Zähler der Ableitung 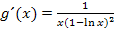kein x vorkommt. Damit eine Funktion ein Extremum haben kann, muss es mindestens einen Punkt mit waagrechter Tangente geben. Es müsste also gelten: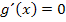

Ein Bruch wird aber bekanntlich nur dann gleich Null, wenn der Zähler gleich Null ist. Die Ableitung 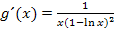kann demnach nicht gleich Null werden, da der Zähler nicht Null werden kann, weil er gar kein x enthält. Deshalb hat die Funktion 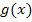sicher keine Extrema.

5. Bsp.:Berechne auf zwei verschiedene Arten die Ableitung von !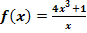

Lösung:

Die Methode, die dir als erstes in den Sinn kommt, ist vermutlich die Verwendung der Quotientenregel. Es handelt sich bei 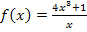schließlich um eine Funktion mit x im Nenner. Das Ableiten mit der Quotientenregel schaffst du bestimmt alleine. Also gleich selbst versuchen! (Zu deiner Kontrolle folgt weiter unten der ausführliche Rechenweg.) Nun stellt sich allerdings die Frage, wie man 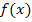auch ohne Verwendung der Quotientenregel ableiten kann. Hast du eine Idee? Nein? Ok, dann forme die Funktion doch erst einmal um, indem du jeden Summanden des Zählers einzeln durch den Nenner teilst.

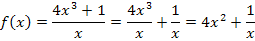
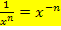Wenn du mit dem Potenzgesetz in eine Potenz umwandelst, also die Umformung 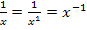durchführst, kannst du die Funktion mit der bekannten Ableitungsregel 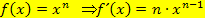bequem ableiten. Danach wendest du noch einmal das Potenzgesetz an, dieses Mal rückwärts, um die Ableitung ohne negativen Exponenten zu schreiben.

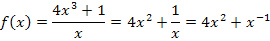
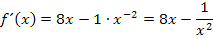
Nun bringen wir noch alles auf einen gemeinsamen Nenner, d.h. wir erweitern bei 8x mit .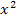

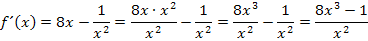
Hier zu deiner Kontrolle noch die andere Methode mit der Quotientenregel.

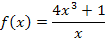
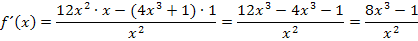
An diesem Beispiel konntest du sehen, dass nicht jede Funktion, die x im Nenner enthält, zwangsläufig mit der Quotientenregel abgeleitet werden muss. Bei Funktionen, deren Nenner keine Summe oder Differenz ist, kann jeder Summand des Zählers einzeln durch den Nenner dividiert und gekürzt werden, so dass man sie danach mit der einfachen Ableitungsregel 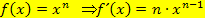differenzieren (= ableiten) kann. Stattdessen kannst du natürlich auch die Quotientenregel anwenden, doch ist das oft mehr Rechenaufwand. Das kommt auf die jeweilige Aufgabe an.

Dies waren hoffentlich genug Beispiele zur Anwendung der Quotientenregel. Gleich weiter mit der dritten neuen Ableitungsregel:Die Kettenregel

---