Die Produktregel

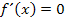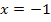Ein Terrassenpunkt kann hier allerdings nicht vorliegen, denn ein Terrassenpunkt ist immer eine doppelte (oder geradfache) Nullstelle der ersten Ableitung, also eine doppelte (vierfache, sechsfache usw.) Lösung der Gleichung . Bei handelt es jedoch um eine einfache Lösung. Deshalb kann ein Terrassenpunkt direkt ausgeschlossen werden. Um nun zu entscheiden, ob ein HOP oder TIP vorliegt, untersuchen wir das Monotonieverhalten von 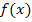. Am besten geht das mit einer Monotonietabelle. (Im Teil Die Ableitungsfunktion 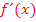wird ausführlich erklärt, wie man eine Monotonietabelle anfertigt.)

Hier noch einmal die Ableitung: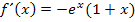

Monotonietabelle:

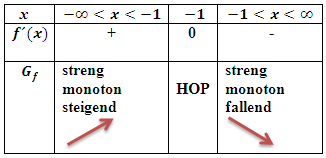
Du verstehst nicht, wie man auf die Vorzeichen in der mittleren Zeile kommt? Dann siehe:Ausführlichere Erklärungen der Monotonietabelle im Bsp. 3b.)

An der Monotonietabelle erkennt man, dass bei 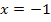ein Hochpunkt (HOP) vorliegen muss, da der Funktionsgraph 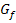für 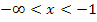steigt 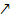und für 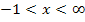fällt 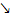. Am Verlauf der Pfeile müsste dir das klar sein. Die y-Koordinate 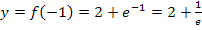haben wir oben schon berechnet. Somit wissen wir, dass die Funktion den folgenden Hochpunkt besitzt: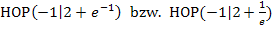 

Nun ist die Aufgabe gelöst.

Das soll uns an Beispielen für die Anwendung der Produktregel genügen. Als nächstes schauen wir uns Die Quotientenregel an.

---