Die Produktregel
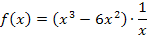
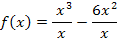
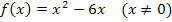
In dieser Form lässt sich die Ableitung nach der Regel 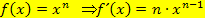 schnell berechnen. Es ergibt sich:
schnell berechnen. Es ergibt sich:
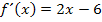
Wer mag, kann noch die Zahl 2 ausklammern.
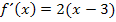
2. Methode:Produktregel anwenden
Bevor wir die Produktregel anwenden, schreiben wir bei der Funktion an Stelle des Bruchs eine Potenz. Wir verwenden dabei das Potenzgesetz 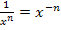 .
.
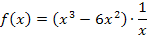
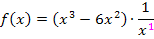
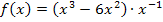
Jetzt wenden wir die Produktregel an, also ersten Faktor ableiten mal zweiten stehen lassen plus ersten Faktor stehen lassen mal zweiten ableiten.
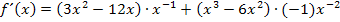
Dies müssen wir jetzt natürlich noch vereinfachen. Wir schreiben statt den Potenzen mit negativen Exponenten wieder Brüche und multiplizieren dann die Brüche jeweils in die Klammern hinein.
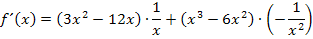
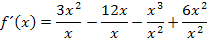
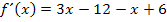
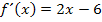
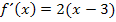
Wir erhalten natürlich wieder die gleiche Ableitung wie oben bei der 1. Methode. Wir setzen sie jetzt gleich Null, um den Punkt mit waagrechter Tangente, in diesem Fall das Extremum, zu finden.
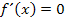
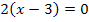
Man erkennt sofort die Lösung: 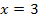
Anmerkung:Man hätte die Gleichung natürlich auch durch folgende Rechnung nach x auflösen können:
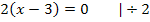
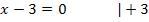
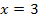
Nun kennen wir die x-Koordinate des Punktes mit waagrechter Tangente. Bei 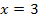 ist ein Punkt mit waagrechter Tangente. Es kann sich dabei um ein Extremum, also einen relativen Hochpunkt (HOP) bzw. einen relativen Tiefpunkt (TIP), handeln oder um einen Terrassenpunkt (TEP). Das müssen wir jetzt untersuchen. Wir verwenden dazu eine Monotonietabelle. (Wie man eine Monotonietabelle anfertigt, wird ausführlich im Teil Die Ableitungsfunktion
ist ein Punkt mit waagrechter Tangente. Es kann sich dabei um ein Extremum, also einen relativen Hochpunkt (HOP) bzw. einen relativen Tiefpunkt (TIP), handeln oder um einen Terrassenpunkt (TEP). Das müssen wir jetzt untersuchen. Wir verwenden dazu eine Monotonietabelle. (Wie man eine Monotonietabelle anfertigt, wird ausführlich im Teil Die Ableitungsfunktion 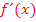 erklärt.)
erklärt.)
Hier noch einmal die Ableitung: 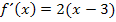
Monotonietabelle:
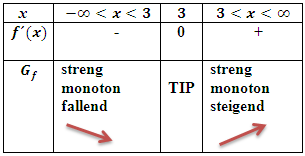
Du verstehst nicht, wie man auf die Vorzeichen in der mittleren Zeile kommt? Dann siehe:Ausführlichere Erklärungen der Monotonietabelle im Bsp. 3a.)
An der Monotonietabelle erkennt man, dass bei 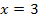 ein Tiefpunkt (TIP) vorliegen muss, da der Funktionsgraph
ein Tiefpunkt (TIP) vorliegen muss, da der Funktionsgraph 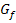 für
für 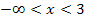 fällt
fällt 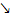 und für
und für 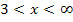 steigt
steigt 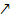 . Am Verlauf der Pfeile müsste dir das klar sein. Die y-Koordinate
. Am Verlauf der Pfeile müsste dir das klar sein. Die y-Koordinate 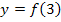 haben wir noch nicht berechnet. Das machen wir jetzt.
haben wir noch nicht berechnet. Das machen wir jetzt.
Wir setzen die x-Koordinate 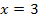 in die Funktionsgleichung
in die Funktionsgleichung 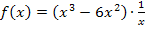 ein.
ein.
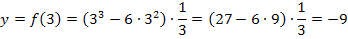
Somit wissen wir, dass die Funktion den folgenden Hochpunkt besitzt: 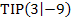
Nun ist die Aufgabe gelöst.
Zu 3b.)
Es sollen Art und Lage des Extremums der Funktion 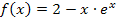 ermittelt werden. Das bedeutet wieder nichts anderes als, dass man die x- und y-Koordinate des Extremums (die Lage des Extremums) herausfinden soll und, ob es sich um einen Hochpunkt (HOP) oder Tiefpunkt (TIP) handelt (die Art des Extremums). Da bei einem Extremum die Tangente an den Graph waagrecht verläuft, muss die Tangentensteigung, also die erste Ableitung, an dieser Stelle gleich Null sein.
ermittelt werden. Das bedeutet wieder nichts anderes als, dass man die x- und y-Koordinate des Extremums (die Lage des Extremums) herausfinden soll und, ob es sich um einen Hochpunkt (HOP) oder Tiefpunkt (TIP) handelt (die Art des Extremums). Da bei einem Extremum die Tangente an den Graph waagrecht verläuft, muss die Tangentensteigung, also die erste Ableitung, an dieser Stelle gleich Null sein.

