Die Produktregel
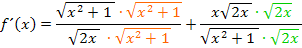
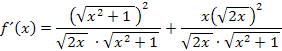
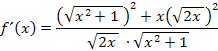
Wurzel und Quadrat heben sich bekanntlich auf, solange der Radikand (= Ausdruck unter der Wurzel) nicht das Quadrat einer negativen Zahl ist. (Vorsicht:Steht unter der Wurzel das Quadrat einer negativen Zahl, heben sich Wurzel und Quadrat nicht einfach auf, man braucht dann noch den Betrag. Bsp.: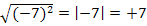 
Dies Problem haben wir bei 
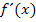aber erfreulicherweise nicht.) Daher heben sich hier Wurzel und Quadrat gegenseitig auf. Es ergibt sich:
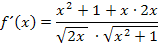
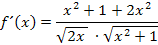
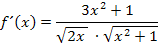
Wir können den Nenner noch unter eine gemeinsame Wurzel schreiben. Vorsicht:Klammer setzen nicht vergessen!
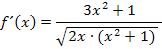
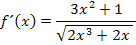
Weiter lässt sich die Ableitung nicht mehr vereinfachen. Juhu! Endlich fertig! Aber gleich weiter mit der nächsten Aufgabe.
3. Bsp.: Berechne Art und Lage des Extremums der Funktion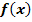 
ohne Verwendung der zweiten Ableitung!
a.)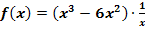 
Ermittle 
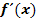dabei auf zwei verschiedene Arten!
b.)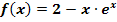 
(Nur für Schüler, die im Unterricht 
bereits behandelt haben.)
Lösung:
Zu 3a.)
Es sollen Art und Lage des Extremums der Funktion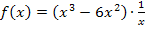 
ermittelt werden. Das bedeutet nichts anderes als, dass man die x- und y-Koordinate des Extremums (die Lage des Extremums) herausfinden soll und, ob es sich um einen Hochpunkt (HOP) oder Tiefpunkt (TIP) handelt (die Art des Extremums). Da bei einem Extremum die Tangente an den Graph waagrecht verläuft, muss die Tangentensteigung, also die erste Ableitung, gleich Null sein.
Extremum: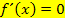 
Manche Lehrer(innen) würden an dieser Stelle über dem Gleichheitszeichen ein kleines Ausrufezeichen schreiben: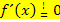 
Das ist streng mathematisch gesehen auch notwendig. Das Gleichheitszeichen mit dem Ausrufezeichen darüber bedeutet so viel wie „soll gleich sein“ oder „es soll gelten, dass…“. Mit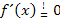 
ist somit gemeint, dass die Ableitung gleich Null sein soll. Du schreibst es am besten genauso wie dein(e) Lehrer(in) in der Schule. Setzt er/sie beim Ansatz das Ausrufezeichen über das Gleichheitszeichen, dann machst du es ebenfalls;schreibt er/sie ein normales Gleichheitszeichen, kannst du das auch so machen. Bei der anschließenden Rechnung wird auf jeden Fall immer ein normales Gleichheitszeichen verwendet.
Die Ableitung soll hier auf zwei verschiedene Arten berechnet werden. Man kann die Funktion 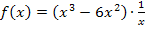entweder direkt mit der Produktregel ableiten – es handelt sich schließlich um ein Produkt, das in beiden Faktoren x enthält – oder die Funktionsgleichung vor dem Ableiten ausmultiplizieren, dann braucht man die Produktregel nicht.
Ableitung bilden:
1. Methode:Zuerst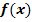 
ausmultiplizieren, dann ableiten
