Die Produktregel

Folgerung:Funktionen, die ein Produkt bilden, worin beide Faktoren die Variable x enthalten, dürfen nicht abgeleitet werden, indem man jeweils die beiden Faktoren einzeln ableitet und dann miteinander multipliziert!

Korrekt ist dagegen die Produktregel.

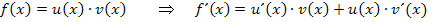
Wir wollen sie noch etwas üben. Daher noch ein paar Beispiele zur Anwendung der Produktregel.

2. Bsp.:Gegeben ist die Funktion 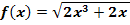mit x 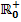. Sie soll nach geeigneter Umformung mit Hilfe der Produktregel abgeleitet werden. Dabei darf als bekannt vorausgesetzt werden, dass gilt:

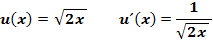
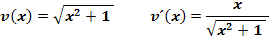
Lösung:

Die Funktion 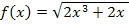stellt an sich gar kein Produkt dar. Damit sie dennoch mit Hilfe der Produktregel abgeleitet werden kann, müssen wir sie erst umformen. Unter der Wurzel klammern wir erst einmal 2x aus.

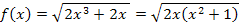
Wie du sicher weißt, gilt: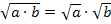

Bei Produkten darf man die Wurzel also einzeln ziehen.

Daher können wir schreiben:

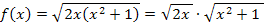
Nun liegt die Funktion als Produkt vor, das in beiden Faktoren die Variable x enthält, so dass sich die Produktregel beim Ableiten verwenden lässt. Die Ableitungen der einzelnen Faktoren sind bereits gegeben. (Du könntest sie selbst momentan noch nicht berechnen, da es sich um verkettete, d.h. ineinander verschachtelte, Funktionen handelt, die nur mit der sogenannten Kettenregel abgeleitet werden können. Die Kettenregel werden wir aber erst später behandeln, vermutlich hast du sie auch im Unterricht noch nicht gelernt. Sie gilt also momentan als unbekannt. Mit Hilfe der Kettenregel könnte die Funktion übrigens auch direkt, also ohne Umformung in ein Produkt, abgeleitet werden. Das wäre eindeutig der schnellere Weg. Doch wir wollen hier schließlich die Produktregel üben.) Nun kann es losgehen mit der Produktregel. Probiere es gleich selbst!

Hier noch einmal alle Angaben auf einen Blick:

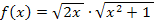
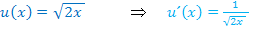
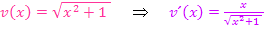
Du müsstest zu folgendem Ergebnis gekommen sein:

Hier noch einmal die Produktregel:

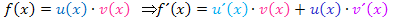
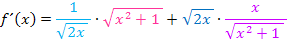
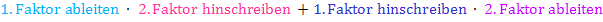
So wie die Ableitung momentan da steht, können wir sie natürlich nicht lassen. Wir müssen sie vereinfachen. Dazu schreiben wir:

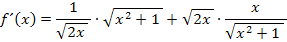
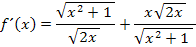
Nun bringen wir alles auf einen gemeinsamen Nenner, damit wir nachher alles auf einen Bruchstrich schreiben können. Der Hauptnenner ist hier 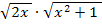. Um den ersten Bruch auf diesen Nenner zu bringen, muss mit 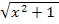erweitert werden. Um den zweiten Bruch auf den Hauptnenner zu bringen, muss mit 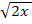erweitert werden. (Wenn du Schwierigkeiten mit dem Erweitern hast, überlegst du dir Folgendes:Wie sieht der ursprüngliche Nenner aus? Was kommt im Vergleich zum Hauptnenner dazu? Mit dem, was dazu kommt, musst du erweitern, d.h. im Zähler damit multiplizieren, wenn du den Bruch auf den Hauptnenner bringen willst.) Weil viele Schüler dabei Probleme haben, schreiben wir das hier ganz besonders ausführlich.

---