Die Produktregel
„Schöner“ wird das Ergebnis allerdings, wenn man den Nenner rational macht, also ohne (dritter) Wurzel schreibt und alles auf einen gemeinsamen Bruchstrich bringt. Um den Nenner rational zu machen, muss hier der Bruch mit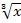 
erweitert werden. (Zur Erinnerung: 
)
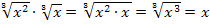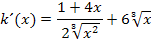
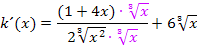
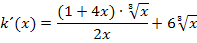
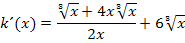
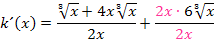
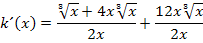
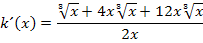
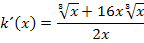
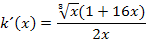
Puh! Endlich fertig!
Zu 1d.) Nur für Schüler geeignet, die im Unterricht die e-Funktion bereits behandelt haben!
Hier noch einmal die Funktionsgleichung: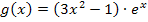 
Es handelt sich, wie schon in den vorherigen Teilaufgaben, um ein Produkt, das in beiden Faktoren die Variable x enthält. Um die Funktion abzuleiten, muss also wieder die Produktregel angewendet werden. Versuche doch gleich mal alleine die Funktion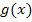 
mit Hilfe der Produktregel abzuleiten:Klammer ableiten mal 
hinschreiben plus Klammer hinschreiben mal ableiten! Weißt du noch, wie man ableitet? Na, klar! abgeleitet ergibt wieder . (Vergleiche auch:Exponentialfunktion!) Also, los geht´s!
Du müsstest auf folgendes Ergebnis gekommen sein:
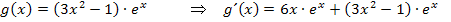
Wir vereinfachen die Ableitung noch, indem wir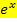 
ausklammern.
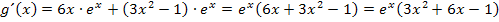
Im letzten Schritt wurden nur die Potenzen in der Klammer nach absteigender Reihenfolge geordnet. Dies ist das Endergebnis, denn weiter lässt sich diese Ableitung nicht vereinfachen.
TIPP:Bei Funktionen mit 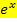bzw.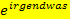 
solltest du 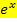bzw. 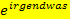immer soweit möglich ausklammern! Die Ableitung lässt sich nämlich bei der Berechnung der Extrema wesentlich besser gleich Null setzen und nach x aufzulösen, wenn man vorher bzw.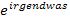 
ausgeklammert hat. Du weißt:Ein Produkt ist gleich Null, wenn einer der Faktoren Null ist. Der Ausdruck bzw. 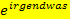ist immer positiv, völlig egal was im Exponenten steht, und kann somit logischerweise niemals gleich Null werden. Es braucht daher nur die Klammer, die durch das Ausklammern entstanden ist, gleich Null gesetzt werden.
Um zum Beispiel die Gleichung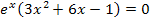 
nach x aufzulösen, muss nur der Ausdruck in der Klammer gleich Null gesetzt und mit der Mitternachtsformelnach x aufgelöst werden. Der Faktor kann nicht Null ergeben und kann somit weggelassen werden. Wenn du die Extrema einer Funktion berechnen sollst, musst man ihre Ableitung bekanntlich immer zuerst gleich Null setzen. Dabei kannst du das gut anwenden.
Zu 1e.) Nur für Schüler geeignet, die im Unterricht die ln-Funktion bereits behandelt haben!
Hier noch einmal die Angabe: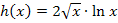 
Hinweis:
Die Ableitung der Wurzelfunktion 
solltest du an sich auswendig wissen.
