Die Kettenregel
Zu Peters drittem Ergebnis: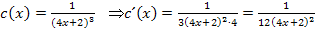 
Auch dieses Ergebnis von Peter ist total falsch. Er hätte entweder Die Quotientenregelin Kombination mit der Kettenregel anwenden müssen, da die Funktion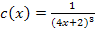 
schließlich ein Bruch mit x im Nenner ist, oder er hätte vor dem Ableiten die im Folgenden gezeigte Umformung der Funktion vornehmen müssen, bevor er 
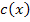nur mit der Kettenregel ableiten kann.
Laut dem Potenzgesetz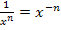 
gilt:
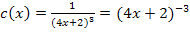
In dieser Form kann die Funktion nur mit der Kettenregel, also ganz ohne Verwendung der Quotientenregel, abgeleitet werden. Das richtige Ergebnis lautet:
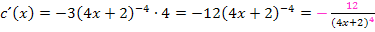
Zum Trost könnte man aber sagen, dass Peter die Kettenregel zumindest bei dieser Aufgabe soweit richtig angewendet hätte, er hat bloßnicht an den Bruch mit x im Nenner gedacht. Wenn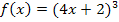 
die gegebene Funktion gewesen wäre, hätte er mit 
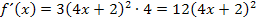absolut richtig gelegen.
Zu Peters viertem Ergebnis:
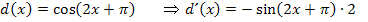
Super, Peter! Da stimmt alles, die äußere Funktion ist bei der Funktion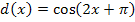 
die Kosinus-Funktion 
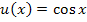. Das ergibt abgeleitet 
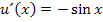. Die innere Funktion von 
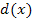ist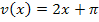 
. Mit ihrer Ableitung 
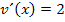wird beim Ableiten von 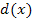zum Schluss multipliziert / nachdifferenziert. Es wird ja bei einer verketteten Funktion zuerst immer die äußere Funktion abgeleitet, wobei statt x die innere Funktion hingeschrieben wird. Dann folgt noch das Nachdifferenzieren mit 
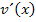, also in diesem Fall mit der Zahl 2.
Zu Peters fünftem Ergebnis: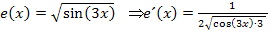 
Das Ergebnis stimmt leider nicht, da ist Peter durcheinander gekommen. Bei der Funktion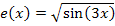 
handelt es sich nämlich um eine doppelt verkettete Funktion. Beim Ableiten solcher Funktionen muss man von außen nach innen ableiten:Die äußerste Funktion, hier die Wurzel wird zuerst abgeleitet, dabei bleibt die innere Funktion der Wurzel, also 
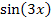, noch stehen. Dann wird 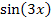nachdifferenziert, d.h. mit der Ableitung davon multipliziert. Da 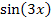selbst auch eine verkettete Funktion ist, darf nur die jetzt äußere Funktion Sinus abgeleitet werden;die jetzt innere Funktion 3x muss noch einmal statt x bei der Ableitung Kosinus hingeschrieben und erst ganz am Schluss noch mal nachdifferenziert werden. Man muss daher gleich zweimal nachdifferenzieren. (Die Ableitung der Wurzelfunktion 
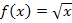ist übrigens von Peter ganz korrekt mit 
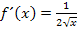ermittelt worden. Er hat dann allerdings den Fahler gemacht, dass er die innere Funktion der Wurzel, also 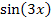, sofort abgeleitet hat. Er hätte die innere Funktion 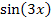erst noch einmal statt dem x in der Ableitung der Wurzel hinschreiben müssen und erst nachher den gesamten bereits ermittelten Ausdruck mit der Ableitung von 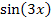, also mit 
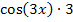multiplizieren müssen.
