Die Kettenregel

Nach diesem Prinzip erhält man beispielsweise auch die Ableitungen der folgenden Funktionen:

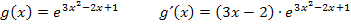
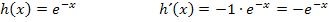
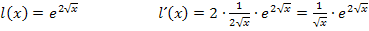
Du siehst, Funktionen der Form „e hoch irgendeine Funktion“ werden abgeleitet, indem man einfach die Ableitung der Funktion im Exponenten bildet und noch mit der ganzen Funktion selbst multipliziert.

Zu 6g.)

Hier noch einmal die Funktion, die abgeleitet werden soll: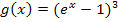

Bei dieser Funktion stellt 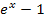die innere Funktion v und die dritte Potenz die äußere Funktion dar. Da 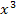nach x abgeleitet 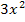ergibt, ist 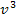nach v abgeleitet 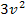. Weil v aber die von x abhängige, innere Funktion 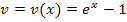darstellt, muss natürlich nachdifferenziert, also mit 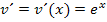multipliziert werden. Somit gilt:

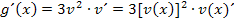
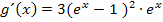
Das ist schon das Endergebnis.

Anmerkung:

Das Quadrat könnte man zwar mit Hilfe der zweiten Binomischen Formelnochausrechnen, doch macht das die Ableitung nicht einfacher. In der Form 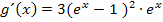lässt sich die Ableitung nämlich leicht gleich Null setzen und nach x auflösen, beispielsweise wenn man die Extrema der Funktion 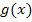berechnen wollte. Es gilt bekanntlich:

Notwendige Bedingung für relative Extrema: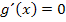

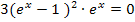
Man müsste sich dann nur überlegen, für welche Werte von x die Klammer 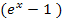Null ergibt. Warum? Wie du sicher weißt, ist ein Produkt gleich Null, wenn einer der Faktoren Null ergibt. Der hintere Faktor unseres Produkts ist immer positiv, so dass nicht gleich Null werden kann. Der Faktor 3 kann sowieso nicht gleich Null sein;es muss also der Ausdruck 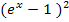gleich Null sein, wenn man die Gleichung 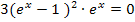lösen wollte. Der Ausdruck 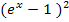ergibt nur dann Null, wenn 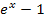gleich Null ist. Man könnte daher bei der Berechnung der Extrema/des Extremums folgendermaßen vorgehen:

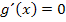
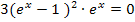
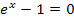
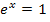
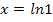
Wenn man dagegen die Ableitung 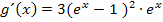mit Hilfe der zweiten Binomischen Formel 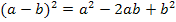ausgerechnet hätte, hätte man die Ableitung in der Form 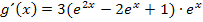oder nach Ausmultiplizieren in der noch unpraktischeren Form 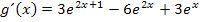vorliegen. Dass sich weder die Gleichung 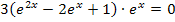noch die Gleichung 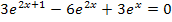schnell nach x auflösen lassen, dürfte einleuchten. Deshalb lassen wir die Ableitung in der nicht ausmultiplizierten Form 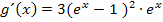stehen und rechnen nicht weiter.

Zu 6h.)

Hier noch einmal die Funktionsgleichung: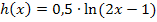

Um diese Funktion abzuleiten, braucht man natürlich wieder die Kettenregel, wobei die ln-Funktion die äußere Funktion und 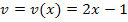die innere Funktion darstellt. Der Faktor 0,5 ist eine multiplikative Konstante, also eine Zahl ohne x, mit der multipliziert wird.

---