Die Kettenregel
Zu 6e.)
Hier noch einmal die Funktionsgleichung: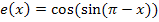 
Diese Funktion hat es in sich. Hier sind nämlich drei Funktionen miteinander verkettet. Die äußerste Funktion ist die Kosinus-Funktion, dann kommt quasi in der Mitte die Sinus-Funktion und ganz innen die Funktion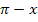 
. Man muss hier praktisch zweimal nachdifferenzieren. Beim Ableiten geht man von außen nach innen vor. Man fängt also beim Ableiten mit dem Kosinus an und lässt dabei erst einmal die (bezüglich dem Kosinus) innere Funktion 
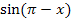stehen, die natürlich noch nachdifferenziert werden muss. Um 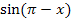abzuleiten, benötigt man aber noch einmal die Kettenregel, weil 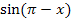selbst noch einmal eine verkettete Funktion ist. Bezüglich dem Sinus ist nämlich 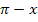die innere Funktion, welche dann noch einmal nachdifferenziert werden muss.
Zur Erinnerung:
So, dann geht´s los.
Geg.: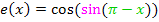 
Kosinus ableiten, dabei innere Funktion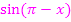 
stehen lassen, dann Sinus ableiten, dabei 
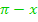stehen lassen und noch einmal mit der Ableitung von 
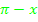nachdifferenzieren.
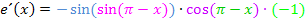
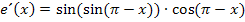
Das war´s schon. Fertig!
Hoffentlich ist dir an diesem Beispiel das Prinzip beim Ableiten mehrfach verketteter Funktionen klar geworden. Immer von außen nach innen ableiten!
Die folgenden Beispiele sind nur für Schüler, die im Unterricht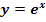 
und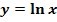 
schon behandelt haben.
Zu 6f.)
Hier noch einmal die Funktionsgleichung: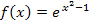 
An sich müsste dir das Prinzip der Kettenregel inzwischen klar sein, doch macht erfahrungsgemäßdie e-Funktion vielen Schülern anfangs Probleme beim Ableiten, wenn sie verkettet ist. Du wirst aber gleich sehen, dass sich gerade Funktionen der Form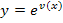 
ganz leicht ableiten lassen.
Bei der Funktion 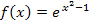ist die e-Funktion die äußere Funktion 
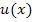und entsprechend 
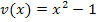die innere Funktion. Wie du weißt, ergibt 
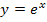abgeleitet wieder 
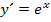. Somit ist 
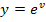(nach v) abgeleitet wieder 
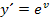. Da v natürlich die von x abhängige, innere Funktion 
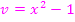darstellt, muss noch mit 
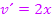nachdifferenziert werden. So ergibt sich für die Ableitung von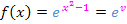 
Viel vereinfachen lässt sich an der Ableitung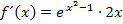 
nicht. Wir betreiben nur noch etwas „Kosmetik“, indem wir die Reihenfolge innerhalb des Produkts umdrehen.
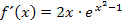
Wir halten fest:Funktionen der Form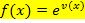 
, wobei 
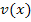die von x abhängige, innere Funktion darstellt, werden abgeleitet, indem man die im Exponenten stehende Funktion 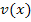ableitet und das Ganze noch mit der ganzen Funktion selbst multipliziert.
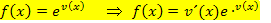
Also:Exponenten ableiten und Funktion dahinter schreiben!
