Die Kettenregel
Deshalb darf man keinesfalls zu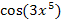 
zusammenfassen! In der umgedrehten Schreibweise 
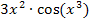ist das vermutlich sowieso klar.
Zu 6c.)
Hier noch einmal die Funktionsgleichung: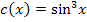 
Wie weiter oben schon erwähnt kann man statt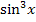 
auch 
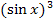schreiben. Beides ist gleichbedeutend. An der letzteren Form erkennt man aber leichter, was innere bzw. äußere Funktion ist. Daher schreiben wir besser 
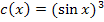. Jetzt solltest du selbst versuchen, die Ableitung 
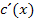zu bilden.
Denk daran:Äußere Funktion ableiten, die innere (statt dem x der äußeren Funktion) hinschreiben und dann mit der Ableitung der inneren Funktion multiplizieren!
Verkettete Funktion: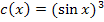
Innere Funktion: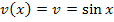 
Äußere Funktion: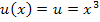 
Die äußere Funktion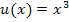 
ergibt nach x abgeleitet 
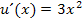. Wir müssen aber 
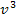ableiten, das ergibt dann 
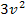. Da v aber die innere Funktion darstellt, muss noch mit v´nachdifferenziert werden. Die gesuchte Ableitung muss somit die Form 
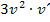haben.
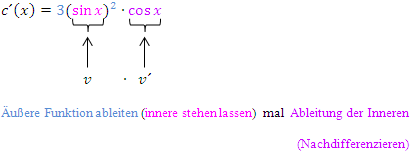
Vereinfachen lässt sich diese Ableitung nicht.
Zu 6d.)
Hier noch einmal die Angabe: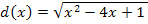 
Inzwischen sollte es dir klar sein, was hier die innere bzw. die äußere Funktion ist. Falls du allerdings nicht mehr auswendig weißt, was die Ableitung der Funktion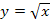 
ist, hier noch der kleine Tipp: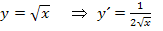 
Jetzt solltest du selbständig versuchen die Ableitung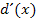 
zu bilden.
Hast du es wirklich alleine versucht? Ok, dann vergleiche dein Ergebnis mit der folgenden Lösung.
Verkettete Funktion: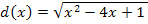
Innere Funktion: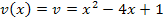 
Äußere Funktion: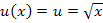 
Ableitung laut Kettenregel: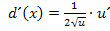 
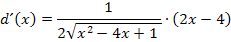
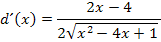
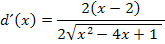
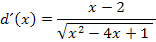
Nicht klar? Dann noch einmal ganz langsam. Bei 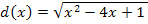muss zuerst die äußere Funktion, also die Wurzel, abgeleitet werden. Weil 
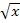abgeleitet 
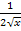ergibt, ist 
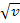abgeleitet 
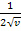. Weil v aber die von x abhängige, innere Funktion 
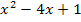darstellt, muss noch nachdifferenziert werde, also mit der Ableitung der inneren Funktion v´ multipliziert werden. Es gilt für die Ableitung von 
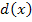somit: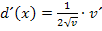 
Mit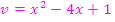 
und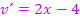 
ergibt sich:
Um die Ableitung zu vereinfachen, schreiben wir alles auf einen gemeinsamen Bruchstrich. Bei der Multiplikation zweier Brüche braucht man keinen Hauptnenner. Man muss nur die beiden Zähler und die beiden Nenner der Brüche jeweils multiplizieren. Den Ausdruck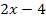 
denken wir uns als Bruch mit dem Nenner 1, also in der Form 
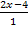, damit es sich offensichtlich um die Multiplikation zweier Brüche handelt. Daher gilt:
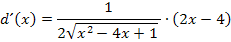
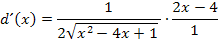
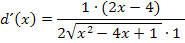
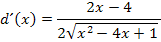
Im Zähler klammern wir nun den Faktor 2 aus, damit wir ihn nachher weg kürzen können.
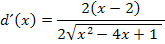
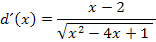
Weiter lässt sich diese Ableitung nicht mehr vereinfachen. Fertig!
