Die Kettenregel

Erst das Ergebnis davon soll hoch 5 gerechnet werden. Zuerst soll also 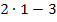gerechnet werden und nicht etwa 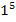. Daher ist 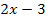die innere Funktion. Wir nennen die innere Funktion 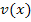, kurz v. Die äußere Funktion nennen wir 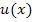, kurz u. Es gilt hier somit:

Verkettete Funktion: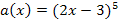

Innere Funktion: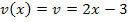 

Äußere Funktion: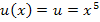

Laut Kettenregel muss zuerst die äußere Funktion abgeleitet werden. 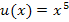ergibt abgeleitet 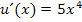. Hätte die Funktion 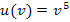gelautet, wäre die Ableitung (nach v) 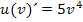. Nun stellt v aber eine von x abhängige Funktion dar. Deshalb muss man nachdifferenzieren, also mit v´multiplizieren. Es gilt: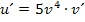

Deshalb ergibt sich für die Ableitung der Funktion :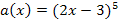

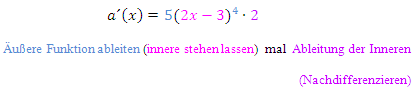
Denke dir beim Ableiten einer verketteten Funktion statt der inneren Funktion ein v und leite dann die äußere Funktion nach v ab. Schreibe zusätzlich hinter den entstandenen Ausdruck „mal v´“. (Das ist das Nachdifferenzieren. Bitte keinesfalls vergessen!) Dabei setzt du für v die innere Funktion ein und für v´die Ableitung der inneren Funktion.

Nun vereinfachen wir die Ableitung noch etwas.

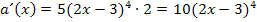
Fertig!

Zu 6b.)

Hier noch einmal die Funktionsgleichung: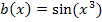

Wir brauchen natürlich wieder die Kettenregel, um die Funktion 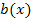abzuleiten. Überlege dir gleich ´mal selbst, was hier die innere bzw. äußere Funktion ist. Frage dich einfach, was man zuerst rechnen muss, wenn man für x etwas einsetzen würde. Zuerst hoch drei oder zuerst den Sinus? Das, was als erstes gerechnet werden soll, stellt die innere Funktion dar.

Es ist dir bestimmt klar, dass hier zuerst hoch 3 und erst nachher der Sinus gerechnet werden soll. Daher stellt die dritte Potenz die innere Funktion dar und die Sinus-Funktion die äußere.

Verkettete Funktion: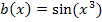

Innere Funktion: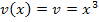

Äußere Funktion: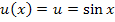

Laut Kettenregel beginnen wir mit der Ableitung der äußeren Funktion. 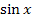ergibt abgeleitet 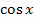;entsprechend ist 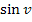(nach v) abgeleitet 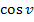. Weil v aber eine von x abhängige Funktion darstellt, müssen wir noch mit v´ nachdifferenzieren.

Die Ableitung von 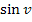ist also .

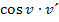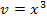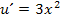Mit und ergibt sich:

Vereinfachen lässt sich diese Ableitung nicht wirklich. Man kann nur die Reihenfolge der Faktoren vertauschen;dies dient aber nur der „Kosmetik“.

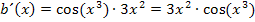
Vorsicht das 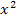und das 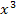hinter dem Kosinus dürfen nicht zu 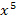zusammengefasst werden! Es steht schließlich kein Malpunkt zwischen 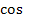und 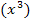. 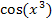bedeutet schließlich „Kosinus von 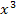“ und eben nicht „Kosinus mal 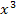“. Im Ausdruck 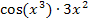bezieht sich der Kosinus nur auf 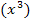, aber nicht auf .

---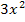