Die Kettenregel

An der letzteren Schreibweise  ist leider nicht so leicht zu erkennen, was innere bzw. äußere Funktion ist. Entsprechendes gilt übrigens auch für Kosinus und Tangens:

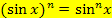
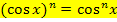
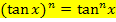
Wenn du später eine Funktion in der Schreibweise 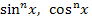gegeben hast, solltest du sie besser in der Form 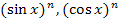schreiben, wenn du sie ableiten sollst. Daran erkennst du besser, was innere bzw. äußere Funktion ist. Der Sinus- bzw. Kosinus ist bei solchen Funktionen die innere und die Potenz die äußere Funktion.

Zu c.)

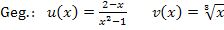
Inzwischen müsste dir das Prinzip bereits klar sein. Wir beginnen wieder mit 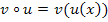. Das heißt, man muss 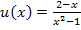(innere Funktion) in 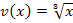(äußere Funktion) für x einsetzen.

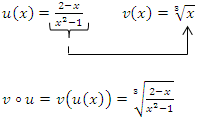
Hier ist also der Bruch die innere und die dritte Wurzel die äußere Funktion.

Jetzt machen wir es wieder genau umgekehrt. Wir bilden 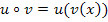. Das heißt, man muss 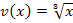(innere Funktion) in 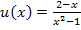(äußere Funktion) für jedes x einsetzen.

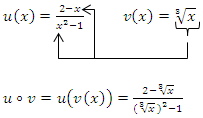
Hier ist also die dritte Wurzel die innere und der Bruch äußere Funktion.

Zu d.)

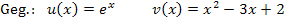
Dieses Mal nur noch schnell die Lösung ohne viele Worte.

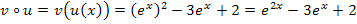
Bei der Umformung 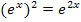wurde das Potenzgesetz 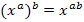verwendet.

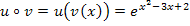
Bei 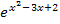ist also die quadratische Funktion 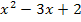die innere Funktion und die e-Funktion die äußere. Funktionen dieser Art wirst du später oft ableiten müssen.

So, nun endlich zur Ableitung verketteter Funktionen. Wir nennen auf dieser website die innere Funktion immer 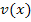. Die äußere Funktion nennen wir 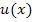. In der Merkhilfe für G8 bzw. FOS wird das genauso geschrieben.

Kettenregel: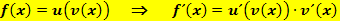

In Worten:Äußere Funktion u ableiten, dabei die innere Funktion v stehen lassen und erst danach mit der Ableitung v´ der inneren Funktion multiplizieren. Das nachträgliche Multiplizieren mit der Ableitung v´der inneren Funktion nennt man Nachdifferenzieren.

Wenn dir die Kettenregel noch gar nicht klar ist, schau´dir erst einmal die folgenden Beispiele an. Daran müsstest du das Prinzip verstehen können.

6. Bsp.:Ermittle die Ableitung der folgenden Funktionen! Vorsicht:Nachdifferenzieren nicht vergessen!

a.)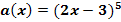

b.)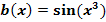

c.)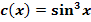

d.)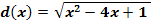

e.)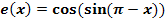

Die Beispiele f.) – i.) sind nur für Schüler, die im Unterricht 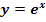und 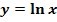schon behandelt haben.

f.)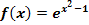

g.)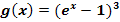

h.)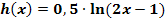

i.)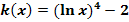

Lösung:

Zu 6a.)

Hier noch einmal die Funktion, die abgeleitet werden soll: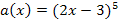

Zuerst müssen wir uns überlegen, was hier innere und äußere Funktion ist. Die innere Funktion erkennst du auch folgendermaßen:Setze für x in die Funktion irgendeine konkrete Zahl ein. Das, was zuerst gerechnet werden muss, ist die innere Funktion. Nehmen wir beispielsweise die Zahl x = 1. Bei 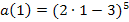muss die Zahl 1 zuerst mit 2 multipliziert und davon 3 abgezogen werden.

---