Unterschied zwischen „Knickwinkel“ und „Schnittwinkel der Tangenten“
Der Schnittwinkel der Tangenten ist grundsätzlich spitz, also kleiner als 90°. Der Schnittwinkel zweier Tangenten ist schließlich ein Schnittwinkel zweier Geraden und dieser ist laut Definition immer spitz. Wenn sich zwei Geraden nicht unter einem 90°-Winkel schneiden, gibt es ja immer einen kleineren und einen größeren Winkel zwischen den beiden Geraden. Damit klar ist, welcher mit „Schnittwinkel der Geraden“ gemeint ist, hat man festgelegt, dass der Schnittwinkel der Geraden grundsätzlich der kleinere der beiden, also der spitze Winkel ist. Sollst du den Schnittwinkel zweier Funktionen berechnen, d.h. den Schnittwinkel der Tangenten an die Funktionen, suchst du daher generell einen Winkel unter 90°. Bekommst du bei der Berechnung von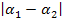 
einen Winkel über 90° heraus, musst du das Ergebnis immer noch von 180° abziehen.
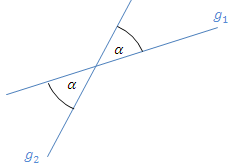
Abb.:Zwei Geraden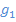 
und 
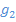mit ihrem Schnittwinkel 
Anders sieht das beim Knickwinkel aus. Der Knickwinkel kann auch stumpf sein. Der Knickwinkel ist nämlich ein Winkel zwischen zwei Halbgeraden und nicht zwischen zwei Geraden! Die eine Tangente hört an der Knickstelle auf und dafür beginnt dort die andere Tangente. Vergleiche dazu die folgenden beiden Abbildungen!
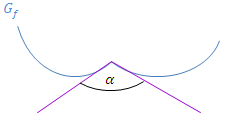
Abb.:Graph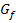 
einer Funktion 
mit Knick und ihren Tangenten an der Schnittstelle (lila), sowie stumpfem Knickwinkel
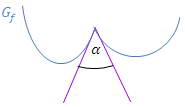
Abb.:Graph 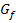einer Funktion mit Knick und ihren Tangenten an der Schnittstelle (lila), sowie spitzem Knickwinkel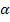
Der Knickwinkel kann somit spitz oder stumpf sein;das hängt ganz vom jeweiligen Verlauf des Graphen in der Umgebung der Knickstelle ab. Er ist aber immer kleiner als 180°.
