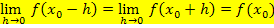Erläuterung der h-Methode für die Überprüfung der Stetigkeit
Eine Funktion ist an der Stelle 
stetig, wenn gilt:
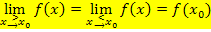
Oder mit der h-Methode:
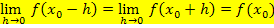
Dabei stellt h eine sehr kleine, positive Zahl dar.
Die beiden gezeigten Ansätze sind gleichbedeutend, denn für die Grenzwerte des Funktionswertes bei linksseitiger bzw. rechtsseitiger Annäherung an die Stelle gilt:
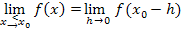
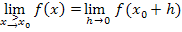
Anschaulich kannst du dir das folgendermaßen vorstellen:
Der Punkt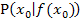 
liegt auf dem Funktionsgraph. (Das ist ein fester, gegebener Punkt, eben genau der Punkt, wo die Stetigkeit untersucht werden soll.) Nun gehen wir von der Stelle etwas nach links bzw. etwas nach rechts und gehen zu den entsprechenden Punkten auf dem Funktionsgraph. Den Abstand von der Stelle nennen wir h. Weil ein Abstand immer positiv ist, muss h positiv sein. Da wir nur ganz wenig nach links und rechts gehen wollen, stellt h eine sehr kleine, positive Zahl dar. Wir gehen also um h nach links bzw. nach rechts. So kommen wir zu zwei Kurvenpunkten:Ein klein wenig links des festen Punktes 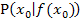liegt der Kurvenpunkt 
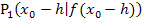und ein klein wenig rechts von 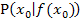liegt der Kurvenpunkt 
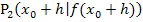. Vergleiche dazu die folgende Abbildung!
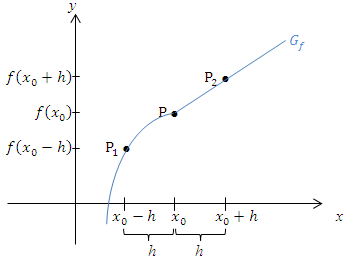
Abb.: Zur Überprüfung der Stetigkeit mit der h-Methode:Graph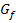 
einer stetigen Funktion
Nun schieben wir die Punkte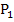 
und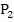 
beliebig nah an den festen Punkt P heran und überprüfen, ob sich dann bei beiden Punkten der gleiche Funktionswert wie bei P ergibt. Dieses Heranschieben der beiden Punkte 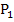und 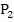an den festen Punkt P bedeutet, dass h immer kleiner wird, also dass h gegen Null geht.
Daher ist eine Funktion stetig, wenn gilt:
