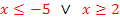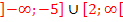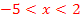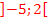Ausführliche Erklärungen zur Lösung der quadratischen Ungleichungen im 2. Bsp.
Wir beginnen mit der folgenden Ungleichung:
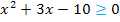
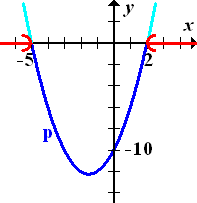
Die Lösungen dieser Ungleichung entsprechen denjenigen Bereichen auf der x-Achse, wo die Parabel oberhalb der x-Achse verläuft, weil wir schließlich die Lösungen der Ungleichung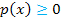 
suchen. In der folgenden Abbildung sind die entsprechenden Parabelstücke hellblau und die zugehörigen Bereiche auf der x-Achse rot markiert. Damit die Ungleichung 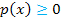erfüllt ist, müssen 
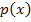bzw. die y-Koordinaten der Punkte auf der Parabel positiv oder gleich Null sein. Das ist genau dann der Fall, wenn die Kurvenpunkte der Parabel oberhalb der x-Achse liegen, bzw. genau in den Parabelpunkten auf der x-Achse. (Punkte, die oberhalb der x-Achse liegen, haben schließlich immer positive y-Koordinaten. Punkte, die genau auf der x-Achse liegen, haben grundsätzlich die y-Koordinate y = 0.) Die Schnittpunkte mit der x-Achse gehören hier gerade noch zur Lösungsmenge dazu, weil in der Ungleichung das Größer-Gleich-Zeichen steht und nicht nur das Größer-Zeichen. Deshalb müssen die Nullstellen der Parabel miteingeschlossen werden. Jetzt entnimmst du der Zeichnung die zugehörigen Bereiche auf der x-Achse. So erhältst du alle Lösungen dieser Ungleichung:
 |
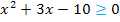
bzw.:
|
Nun zur zweiten Ungleichung:
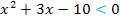
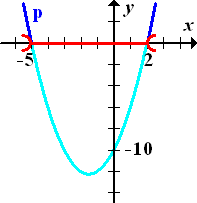
Die Lösungen dieser Ungleichung entsprechen dann logischerweise denjenigen Bereichen auf der x-Achse, wo die Parabel unterhalb der x-Achse verläuft, weil wir jetzt schließlich die Lösungen der Ungleichung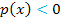 
suchen. In der nächsten Abbildung (unten) sind die entsprechenden Parabelstücke wieder hellblau und die zugehörigen Bereiche auf der x-Achse rot markiert. Damit die Ungleichung 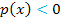erfüllt ist, müssen 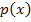bzw. die y-Koordinaten der Punkte auf der Parabel negativ sein. Das ist genau dann der Fall, wenn die Kurvenpunkte der Parabel unterhalb der x-Achse liegen. (Punkte, die unterhalb der x-Achse liegen, haben schließlich immer negative y-Koordinaten.) Die Schnittpunkte mit der x-Achse gehören hier gerade nicht mehr zur Lösungsmenge dazu, weil in der Ungleichung das Kleiner-Zeichen steht und eben nicht das Kleiner-Gleich-Zeichen. Deshalb müssen jetzt die Nullstellen der Parabel ausgeschlossen werden. Jetzt kannst du bestimmt aus der Zeichnung die zugehörigen Bereiche auf der x-Achse ablesen. So erhältst du alle Lösungen der Ungleichung:
 |
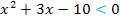
bzw.:
|
Wenn du speziellere Informationen zu den verschiedenen Lösungsmöglichkeiten (z. B. auch zum rein rechnerischen Verfahren) quadratischer Ungleichungen suchst, gehe zu:Quadratische Ungleichungen
