Stetigkeit und Differenzierbarkeit
Hier noch einmal die Funktion in ihrer betragsfreien Form:
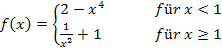
Allgemeiner Ansatz der h-Methode für die Annäherung von links an die Stelle 
:
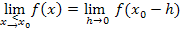
In dieser Aufgabe gilt: 
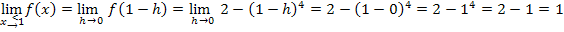
Anmerkung:Um in diesem Beispiel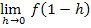 
zu berechnen, muss die Teilfunktion 
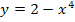verwendet werden, da man sich schließlich von links an die Nahtstelle annähert und diese Teilfunktion für 
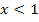gilt. Man ersetzt dann jedes in 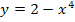vorkommende x durch 
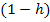und setzt dann für h die Zahl 0 ein.
Allgemeiner Ansatz der h-Methode für die Annäherung von rechts an die Stelle :
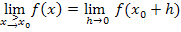
In dieser Aufgabe gilt:
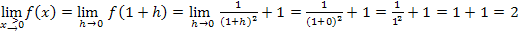
Anmerkung:Um in diesem Beispiel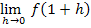 
zu berechnen, muss die Teilfunktion 
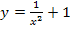verwendet werden, da man sich schließlich von rechts an die Nahtstelle annähert und diese Teilfunktion für 
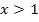gilt. Man ersetzt dann jedes in 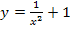vorkommende x durch 
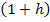, vereinfacht soweit möglich und setzt dann für h die Zahl 0 ein.
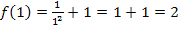
Um den Funktionswert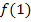 
zu bilden, muss man schauen, bei welcher der beiden Teilfunktionen 
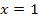mit eingeschlossen ist, also bei welcher Teilfunktion das Gleichheitszeichen bei dem Ungleichheitszeichen dabei ist.
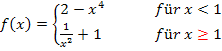
Hier ist das bei der unteren der beiden Teilfunktionen der Fall. Deshalb muss man 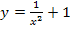benutzen, um 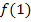zu berechnen.
Noch einmal alle Ergebnisse übersichtlich zusammengefasst:
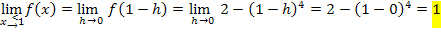
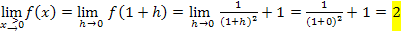
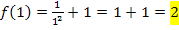
Die drei Ergebnisse sind nicht gleich, daher ist die Funktion 
an der Stelle nicht stetig. Der Graph hat hier also eine Sprungstelle. (Das haben wir ja auch schon vorher bei der 1. Methode herausgefunden.)
2. Bsp.:
Untersuche die Funktion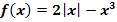 
auf Stetigkeit an der Stelle 
!
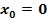Lösung:
Um die Funktion auf Stetigkeit untersuchen zu können, muss sie erst mal betragsfrei geschrieben werden. Man muss also den Betrag auflösen.
Zur Erinnerung:Wenn x positiv oder gleich Null ist, kann der Betrag bei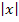 
weggelassen werden;man schreibt für 
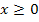einfach bloßx (ohne Betrag). Ist x aber negativ, muss statt 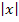der Ausdruck 
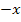geschrieben werden. (Der Betrag macht eine Zahl ungleich Null schließlich immer positiv; der Betrag von Null ist wieder Null. Der Betrag einer beliebigen Zahl ist immer positiv oder Null, aber niemals negativ. Stellt x eine negative Zahl dar, ist 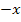entsprechend positiv. Deshalb schreibt man für x <0 eben 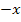statt 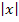.) Mit diesen Überlegungen ergibt sich die betragsfreie Form:
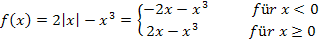
Ob man das Gleichheitszeichen bei der oberen oder unteren Teilfunktion dazu nimmt, ist an sich egal.
