Stetigkeit und Differenzierbarkeit

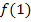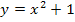Den Funktionswert erhält man in diesem Beispiel durch Einsetzen von in die Parabel , da sie für 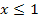definiert ist. (Das Gleichheitszeichen unter dem Kleiner-Zeichen ist hierbei entscheidend!)

2. Methode, die sogenannte „h-Methode“ (vor allem für Schüler einer FOS wichtig)

Hier noch einmal unsere Beispielfunktion:

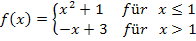
Bei dieser Methode werden die beiden benötigten Grenzwerte (Annäherung von links und von rechts an die Stelle ), nicht durch bloßes Einsetzen von in die beiden Teilfunktionen berechnet, sondern auf folgende Art und Weise:

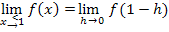
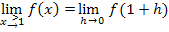
h steht dabei für eine sehr kleine, aber positive Zahl. Es gilt also: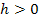

In diesem Beispiel befindet sich die Nahtstelle bei . Wenn man bei den oben gezeigten Grenzwerten die Zahl 1 durch die allgemeine Bezeichnung der Nahtstelle ersetzt, erhält man den allgemeinen Ansatz der h-Methode zur Überprüfung der Stetigkeit an der Stelle .

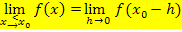
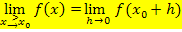
Du willst wissen, woher diese Ansätze kommen? Dann gehe zu:Erläuterung der h-Methode für die Überprüfung der Stetigkeit

Nun aber wieder zu unserem konkreten Beispiel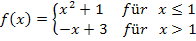

Beginnen wir mit der Annäherung von links an die Nahtstelle , also mit dem linksseitigen Grenzwert.

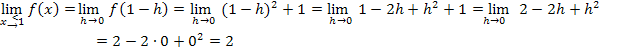
Erklärung der einzelnen Rechenschritte:

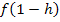wird gebildet, indem man in die Teilfunktion, die für 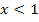gilt, also hier in die Parabelgleichung 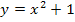für x den Ausdruck 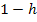einsetzt. (Wäre x in der jeweiligen Teilfunktion mehrmals vorgekommen, hätte jedes x durch 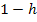ersetzt werden müssen.) Deshalb gilt: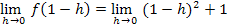

Dann wird der Ausdruck 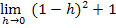soweit möglich vereinfacht. In diesem Fall wird dabei die zweite binomische Formel 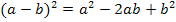verwendet, um die Klammer zu quadrieren. Es ergibt sich: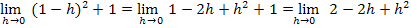

Den Grenzwert 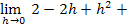berechnet man dann, indem man einfach für h genau die Zahl 0 einsetzt. So ergibt sich: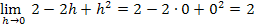

Entsprechend gehen wir jetzt bei der rechtsseitigen Annäherung an die Stelle vor. Dabei muss allerdings die andere Teilfunktion verwendet werden, also diejenige, die für 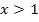gilt, d.h. in diesem Beispiel die Gerade 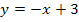. Es gilt schließlich:

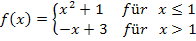
Um 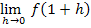zu berechnen, wird in 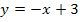für x der Ausdruck 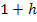eingesetzt.

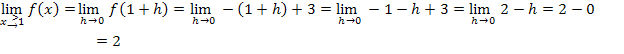
Bei beiden Grenzwerten kommt dasselbe Ergebnis, nämlich der Wert 2, heraus. Auch für den Funktionswert gilt: 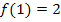. (Der Funktionswert 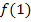wird berechnet, indem man die Zahl 1 in die Parabelgleichung 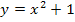einsetzt. Es wird an der Stelle die Parabelgleichung verwendet und nicht die Gerade, weil in der Funktionsgleichung von bei der Parabel das „Kleiner-Gleich-Zeichen“ steht.

---