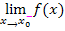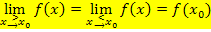Stetigkeit und Differenzierbarkeit
Welche Methode du anwenden musst, hängt einzig und allein von deinem Lehrer in der Schule ab. So wie ihr es in der Schule gemacht habt, so musst du es auch in den Prüfungen machen. (An der Universität ist noch ein anderes Verfahren, die sogenannte 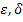 -Methode, gebräuchlich. Sie ist für Abiturient(inn)en nicht geeignet. Da auf dieser website ausschließlich der Mathe-Schulstoff bis zum Abitur behandelt wird, wird hier auf die Erläuterung der
-Methode, gebräuchlich. Sie ist für Abiturient(inn)en nicht geeignet. Da auf dieser website ausschließlich der Mathe-Schulstoff bis zum Abitur behandelt wird, wird hier auf die Erläuterung der 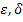 -Methode verzichtet.)
-Methode verzichtet.)
2. Rechnerische Überprüfung von Stetigkeit und Differenzierbarkeit an der Stelle 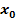
2a.) Überprüfung der Stetigkeit
Hauptsächlich bei teilweise definierten Funktionen (= aus mehreren Teilfunktionen zusammengesetzte Funktionen, oft mit geschweifter Klammer geschrieben) wird ab der 11. Klasse die rechnerische Überprüfung der Stetigkeit verlangt. Dies kann entweder mit Hilfe der h-Methode oder wesentlich einfacher durch bloßes Einsetzen des Wertes  in die jeweiligen Teilfunktionen geschehen. Ergibt sich dabei immer das gleiche Ergebnis, ist die Funktion dort stetig.
in die jeweiligen Teilfunktionen geschehen. Ergibt sich dabei immer das gleiche Ergebnis, ist die Funktion dort stetig.
Mathematisch korrekt formuliert:Sind der linksseitige Limes von  für x gegen
für x gegen  , der rechtsseitige Limes von
, der rechtsseitige Limes von  für x gegen
für x gegen  und der Funktionswert
und der Funktionswert 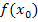 gleich, ist die Funktion an der Stelle
gleich, ist die Funktion an der Stelle  stetig.
stetig.
Definition: Eine Funktion  ist an der Stelle ist an der Stelle   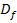 stetig, wenn gilt: stetig, wenn gilt:
|
Anmerkung:
 steht dabei für eine konkrete Zahl. Eine Funktion wird immer lokal, also an einer bestimmten Stelle
steht dabei für eine konkrete Zahl. Eine Funktion wird immer lokal, also an einer bestimmten Stelle  auf Stetigkeit untersucht. In unserem Beispiel ist
auf Stetigkeit untersucht. In unserem Beispiel ist  . Mit
. Mit  ist also die Nahtstelle gemeint, an der die Intervalle der Teilfunktionen einer teilweise definierten Funktion zusammenstoßen.
ist also die Nahtstelle gemeint, an der die Intervalle der Teilfunktionen einer teilweise definierten Funktion zusammenstoßen.
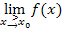 Sprich:„Limes von x gegen
Sprich:„Limes von x gegen  von rechts der Funktion
von rechts der Funktion 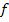 von x“
von x“
Das Größer-Zeichen über dem Pfeil zwischen x und  bedeutet:Annäherung an die Stelle
bedeutet:Annäherung an die Stelle  von rechts. x ist also etwas größer als der feste Zahlenwert
von rechts. x ist also etwas größer als der feste Zahlenwert  . Man nähert sich daher von rechts an die Nahtstelle
. Man nähert sich daher von rechts an die Nahtstelle  an. (Rechtsseitiger Grenzwert) Manche Lehrer verwenden dafür auch die folgende Schreibweise:
an. (Rechtsseitiger Grenzwert) Manche Lehrer verwenden dafür auch die folgende Schreibweise: 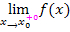 oder
oder 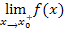
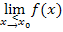 Sprich:„Limes von x gegen
Sprich:„Limes von x gegen  von links der Funktion
von links der Funktion 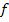 von x“
von x“
Das Kleiner-Zeichen über dem Pfeil zwischen x und  bedeutet:Annäherung an die Stelle
bedeutet:Annäherung an die Stelle  von links. x ist also etwas kleiner als der feste Zahlenwert
von links. x ist also etwas kleiner als der feste Zahlenwert  . Man nähert sich daher von links an die Nahtstelle
. Man nähert sich daher von links an die Nahtstelle  an. (Linksseitiger Grenzwert) Manche Lehrer verwenden dafür auch die folgende Schreibweise:
an. (Linksseitiger Grenzwert) Manche Lehrer verwenden dafür auch die folgende Schreibweise: 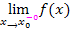 oder
oder