Stetigkeit und Differenzierbarkeit
Jede Parabel ist eine Polynomfunktion (zweiten Grades) und ist daher für sich alleine genommen stetig und differenzierbar. Jede schräge Gerade ist ebenfalls eine Polynomfunktion (ersten Grades) und somit für sich alleine betrachtet auch stetig und differenzierbar. Das Problem ist allerdings die Nahtstelle. Bei einer teilweise definierten Funktion gibt es zwei Fragen, die geklärt werden müssen:
1. Gehen die beiden Teilfunktionen an der Nahtstelle 
ohne Sprung ineinander über? In anderen Worten:Ist die Funktion an der Stelle stetig?
2. Wenn sie dort stetig ist:Gehen die Teilfunktionen an der Nahtstelle ohne Knick, d.h. weich ineinander über? In anderen Worten:Ist die teilweise definierte Funktion bei differenzierbar?
Anmerkung:Mit „differenzierbar an der Stelle “ ist gemeint, dass die Funktion „an der Stelle einmal differenzierbar“ ist. Es geht also darum, ob die erste Ableitung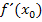 
existiert, d.h. ob die Steigung an der Stelle angegeben werden kann. Man könnte natürlich auch untersuchen, ob die Funktion mehrmals, z. B. zweimal bzw. dreimal differenzierbar ist. Dann geht es darum, ob die zweite Ableitung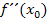 
bzw. die dritte Ableitung 
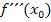existiert. Wir wollen im Folgenden jedoch ausschließlich untersuchen, ob eine teilweise Funktion an der Stelle stetig und einmal differenzierbar ist.
Stetigkeit und Differenzierbarkeit sind eigentlich lokale Eigenschaften;d.h. wir untersuchen die Funktion immer an einer bestimmten Stelle, wie schon gesagt an der Nahtstelle . Manchmal gibt es sogar mehrere Nahtstellen, dann muss jede Stelle einzeln untersucht werden.
Wir bleiben aber erst einmal bei unserem Einführungsbeispiel: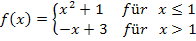 
Hier gibt es natürlich nur eine Nahtstelle, nämlich bei 
. Ist die Funktion dort stetig und differenzierbar?
Wir nähern uns dem Problem von der anschaulichen Seite und skizzieren erst einmal den Graph 
.
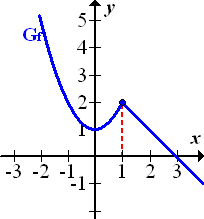
Abb.:Graph der Funktion
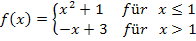
Man erkennt an der Skizze sofort, dass bei zwar keine Sprungstelle, aber ein Knick vorliegt, dass die Funktion bei also stetig ist, aber nicht differenzierbar. Das muss allerdings noch rechnerisch nachgewiesen werden. (Ausführliche Erklärung folgt weiter unten.) Dazu stehen uns die aufwendige h-Methode zur Verfügung oder die viel kürzere Methode, einfach die Nahtstelle in beide einzelnen Teilfunktionen einzusetzen.
