Stetigkeit und Differenzierbarkeit
Die zweite Gleichung bekommst du, indem du die zwei Ergebnisse der Grenzwerte, die du bei der Differenzierbarkeit berechnet hast, ebenfalls gleichsetzt.
Hier noch einmal die Funktion: 
Stetigkeit:
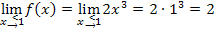
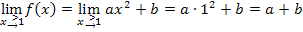
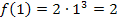
Weil die Funktion an der Stelle  stetig sein soll, müssen die Ergebnisse der Grenzwerte
stetig sein soll, müssen die Ergebnisse der Grenzwerte 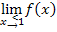 und
und  gleich sein. Wir setzen sie deshalb gleich. So erhalten wir die erste Gleichung:
gleich sein. Wir setzen sie deshalb gleich. So erhalten wir die erste Gleichung:

Differenzierbarkeit:
Hier noch einmal die Funktion: 
Wir bilden ihre Ableitung: 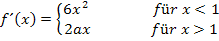
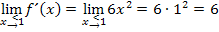
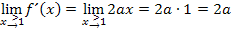
Weil die Funktion an der Stelle  differenzierbar sein soll, müssen auch die Ergebnisse der Grenzwerte
differenzierbar sein soll, müssen auch die Ergebnisse der Grenzwerte 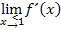 und
und  gleich sein. Wir setzen nun auch die Ergebnisse dieser Grenzwerte gleich. So erhalten wir die zweite Gleichung:
gleich sein. Wir setzen nun auch die Ergebnisse dieser Grenzwerte gleich. So erhalten wir die zweite Gleichung:
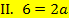
Nun liegt ein Gleichungssystem aus zwei Gleichungen für die zwei Unbekannten a und b vor.

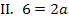
Erfreulicherweise enthält II. nur die Unbekannte a, so dass sich a daraus direkt berechnen lässt. Wir lösen II. nach a auf;dann kennen wir a. Das Ergebnis setzen wir dann in I. ein und können damit b ermitteln.
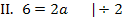

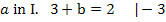
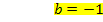
Damit ist die Aufgabe gelöst! Für a = 3 und b = -1 ist die Funktion an der Stelle  stetig und differenzierbar.
stetig und differenzierbar.
Anmerkung:Nicht bei allen Aufgaben dieses Typs lassen sich a und b so leicht ermitteln. Bei manchen Aufgaben ergibt sich nämlich ein Gleichungssystem, das in keiner der beiden Gleichungen nur eine Unbekannte enthält;in beiden Gleichungen kommen also beide Unbekannten vor. Dann muss das Gleichungssystem mit Hilfe des Einsetzungs- oder Additionsverfahrens gelöst werden. Näheres dazu auch im Kapitel Gleichungssysteme:Zwei Gleichungen für zwei Unbekannte
Manchmal ist die Aufgabe auch anders formuliert. Beispielsweise könnte man auch schreiben:„Bestimme die Koeffizienten a und b so, dass der Graph der Funktion  ohne Sprung und ohne Knick verläuft!“ Das ist das gleiche wie „Bestimme die Koeffizienten a und b so, dass die Funktion
ohne Sprung und ohne Knick verläuft!“ Das ist das gleiche wie „Bestimme die Koeffizienten a und b so, dass die Funktion  stetig und differenzierbar ist“.
stetig und differenzierbar ist“.
Dies soll uns hier an Beispielen rund um das Thema Stetigkeit und Differenzierbarkeit genügen. Üben musst du natürlich selbst. Aufgaben findest du bestimmt in deinem Mathebuch.
- Page 32 of 32
- « Previous
- 29
- 30
- 31
- 32
- Next »

