Stetigkeit und Differenzierbarkeit
Mit der Formel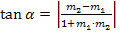 
wird der Schnittwinkel zweier Geraden mit den Steigungen 
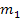und 
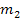berechnet. Wir suchen hier aber den Knickwinkel.
Vorsicht:Der Schnittwinkel der Tangenten, also der Winkel, welcher sich aus der Formel ergibt, ist nur dann identisch mit dem gesuchten Knickwinkel, wenn der Knickwinkel nicht über 90° großist! Derjenige Winkel, welcher mit der oben gezeigten Formel berechnet wird, ist immer ein spitzer Winkel, also zwischen 0° und 90°. Aus der Formel ergibt sich schließlich der Schnittwinkel der beiden Tangenten und ein Schnittwinkel zweier Geraden ist laut Definition immer spitz. Siehe auch:Unterschied zwischen „Knickwinkel“ und „Schnittwinkel der Tangenten“
Der gesuchte Knickwinkel kann dagegen auch stumpf sein, also über 90° bis 180° groß! Ob der jeweilige Knickwinkel kleiner oder größer als 90° ist, überlegt man sich am besten an einer Skizze des Graphen mit den Tangenten an der Knickstelle! Ist der Knickwinkel größer als 90°, muss der vorher mit der großen Formel berechnete Winkel noch von 180° abgezogen werden. Ist der Knickwinkel kleiner als 90°, ergibt sich mit der großen Formel direkt der gesuchte Knickwinkel.
Die Formel 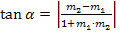liefert also nicht immer den gesuchten Knickwinkel, sondern manchmal nur den Nebenwinkel des Knickwinkels.
Merke:Immer eine Skizze des Graphen mit den Tangenten an der Knickstelle anfertigen und kontrollieren, ob der Knickwinkel über oder unter 90° großist!
Jetzt aber wieder zu unserem Beispiel.
Hier noch einmal unsere Funktion: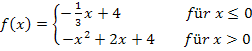 
Bei der Überprüfung der Differenzierbarkeit haben wir die Grenzwerte der Ableitung an der Stelle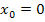 
schon berechnet. Die Ergebnisse entsprechen den Steigungen 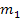und 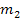der Tangenten von links und von rechts an der Knickstelle. Welchen Grenzwert man mit 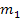bzw. mit 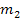bezeichnet, ist egal. Durch den Betrag auf der rechten Seite der Formel ist immer sichergestellt, dass die rechte Seite unabhängig von der Wahl der Bezeichnungen 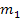und 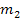etwas Positives ergibt. Wir entscheiden uns für die folgende Benennung:
(Man hätte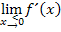 
aber genauso gut mit 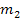bezeichnen können und 
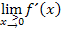mit .)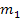
Wir setzen in die Formel ein und berechnen damit den Schnittwinkel der Tangenten.
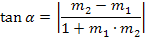
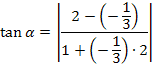
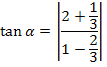
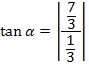
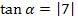
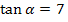
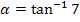
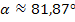
(Bei der 1. Methode ergab sich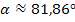 
dies ist nur ein Rundungsfehler!)
Nun muss man sich überlegen, ob der berechnete Winkel schon der gesuchte Knickwinkel ist, oder ob man den berechneten Winkel noch von 180° abziehen muss. Dazu benötigen wir eine Skizze des Graphen mit den Tangenten an der Knickstelle.
