Stetigkeit und Differenzierbarkeit
Wir haben vorher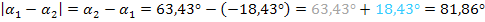 
gerechnet. Auf unserer Skizze bezogen bedeutet das, dass der graue und der hellblaue Winkel zusammen den berechneten 81,86°-Winkel ergeben. Der gesuchte Knickwinkel ist jedoch der rosafarbene Winkel, also der Nebenwinkel des 81.86°-Winkels.
Um den gesuchten Knickwinkel zu erhalten, müssen wir den vorher berechneten 81,86°-Winkel noch von 180° abziehen. (Winkel und zugehöriger Nebenwinkel ergänzen sich bekanntlich immer zu 180°.)
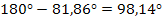
Der Knickwinkel beträgt somit 98,14°. Es handelt sich um einen stumpfen Winkel. Man kann das an der Abbildung wahrscheinlich nicht so deutlich erkennen, weil der Winkel nur relativ wenig über 90° ist. Wenn du jedoch ein Geodreieck zu Hilfe nimmst, wirst du tatsächlich feststellen, dass der gesuchte Knickwinkel (in der Abbildung oben rosa) wirklich stumpf ist. Der zuerst berechnete Winkel von 81,86° ist dagegen spitzt;es war noch nicht der richtige Winkel.
Hinweis:In diesem Beispiel ist der Knickwinkel nicht identisch mit dem Schnittwinkel der Graphen, d.h. dem Schnittwinkel der Tangenten an der Knickstelle. Der Knickwinkel (rosa in der Abbildung oben) ist hier der Nebenwinkel des Schnittwinkels der Tangenten (in der obigen Abbildung:grauer und hellblauer Winkel zusammen).
Dir ist noch nicht klar, worin genau der Unterschied zwischen dem Knickwinkel und dem Schnittwinkel der Tangenten an der Knickstelle, d.h. dem Winkel zwischen zwei Geraden, liegt? Dann siehe:Unterschied zwischen „Knickwinkel“ und „Schnittwinkel der Tangenten“
Nun aber auch zur vorher schon erwähnten 2. Methode. Gerade für diese Methode ist der feine Unterschied zwischen Knickwinkel und Schnittwinkel der Tangenten wichtig.
|
Für Schüler einer FOS technischer Zweig:
2. Methode zur Berechnung des Knickwinkels Bei der Untersuchung der Differenzierbarkeit an der Stelle Wir bezeichnen die Ergebnisse dieser Grenzwerte mit
Für den Schnittwinkel zwischen zwei Geraden mit den Steigungen
Ergebnisse der Grenzwerte D.h. den Ausdruck auf der rechten Seite der Formel z.B. mit dem Taschenrechner ausrechnen und dann im Mode DEG die Tastenfolge Shift tan Ans = verwenden. („Ans“ steht hierbei für das vorher berechnete Zwischenergebnis der rechten Seite.) Achtung: Die Formel liefert immer einen spitzen Winkel. Da der Knickwinkel manchmal aber stumpf ist, ergibt sich mit der Formel nicht immer direkt der gesuchte Knickwinkel, sondern nur den Schnittwinkel der beiden Tangenten! Siehe auch:Unterschied zwischen „Knickwinkel“ und „Schnittwinkel der Tangenten“ Deshalb Skizze des Graphen mit den Tangenten an der Knickstelle anfertigen und kontrollieren, ob der Knickwinkel in der jeweils vorliegenden Aufgabe über oder unter 90° großist! Wenn der gesuchte Knickwinkel kleiner als 90° ist:Der Winkel, der sich aus der Formel ergibt, ist direkt der gesuchte Knickwinkel. Wenn der gesuchte Knickwinkel größer als 90° ist:Der Winkel, der sich aus der Formel ergibt, ist nicht direkt der gesuchte Knickwinkel. Der mit der Formel berechnete Winkel muss noch von 180° abgezogen werden. Wenn du mit der Formel nicht weiterkommst, weil der Nenner beim Einsetzen der Werte Erinnere dich an die Formel Schneiden sich die Tangenten an der Knickstelle unter einem Winkel von 90°, gilt für die Tangentensteigungen Der Nenner der Formel |
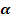an der Stelle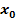 
wurden bereits die beiden Grenzwerte der Ableitung 
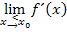und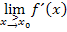 
berechnet.
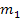und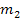 
. Diese beiden Ergebnisse stellen die Tangentensteigungen von links bzw. von rechts dar.
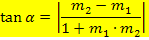
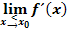und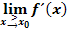 
jeweils für 
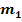bzw.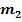 
in diese Formel einsetzen 
Schnittwinkel der linksseitigen und der rechtsseitigen Tangente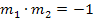
für zueinander senkrechte Geraden!
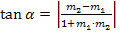wird dann gleich Null. Daher gilt die Formel nur für 
.
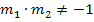