Stetigkeit und Differenzierbarkeit
Dann brauchst du keinen Betrag. (Der Betrag steht hier nur, damit sicher etwas Positives herauskommt. Man kann schließlich nicht generell sagen, welcher Winkel der größere ist. Mit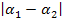 
ist eigentlich gemeint, dass man von 
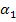den Winkel 
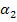abziehen soll, wenn 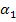der größere der beiden Winkel ist, und umgekehrt von 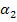den Winkel 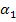abziehen soll, wenn 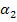der größere der beiden Winkel ist.)
In diesem Beispiel gilt: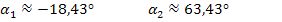 
Hier ist also 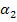der größere Winkel. Daher rechnen wir: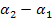 
Vorsicht:Der Winkel 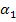ist negativ! Aus Minus Minus ergibt sich daher Plus!
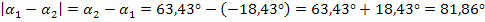
Jetzt muss jedoch noch die Frage geklärt werden, ob der berechnete Winkel von 81,86° bereits der gesuchte Knickwinkel ist, oder ob es sich dabei bloßum den Nebenwinkel des Knickwinkels handelt und man das Ergebnis noch von 180° abziehen muss, um auf den Knickwinkel selbst zu kommen.
Ohne Skizze der Tangenten an der Knickstelle lässt sich diese Frage nicht beantworten. Auf den exakten Verlauf des Graphen selbst kommt es gar nicht an. Eine grobe Skizze reicht völlig. Entscheidend sind die Tangentensteigungen, in diesem Beispiel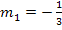 
für die linksseitige Tangente und 
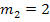für die rechtsseitige Tangente im Punkt (0|4). Hinweis:Die y-Koordinate y = 4 des Kurvenpunktes, wo der Knick ist, wurde bei der Untersuchung der Stetigkeit schon mit f (0) = 4 berechnet.
Um die linksseitige Tangente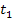 
zu zeichnen, müsste man von (0|4) ausgehen und das Steigungsdreieck zeichnen:Wegen 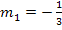würde man dabei 3 nach rechts und 1 nach unten oder 3 nach links und 1 nach oben gehen. Besser hier 3 nach links und 1 nach oben gehen, denn diese Tangente darf nur links vom Punkt (0|4) gezeichnet werden. Es handelt sich bei 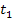schließlich um die linksseitige Tangente an der Stelle 
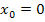. In diesem Beispiel fällt diese Tangente natürlich mit dem Graph 
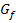zusammen, weil der Graph 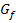für x <0 eine Gerade ist. (Die „Tangente an eine Gerade“ ist praktisch die Gerade selbst.) Die Tangente 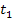muss hier also nicht extra eingezeichnet werden, wenn man vorher den gesamten Graph 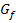bereits skizziert hat.
Die rechtsseitige Tangente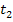 
muss aber wirklich eingezeichnet werden. Man geht dazu vom Punkt (0|4) aus und zeichnet ein Steigungsdreieck:Wegen 
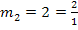geht man 1 nach rechts und 2 nach oben. Diese Tangente darf natürlich nur rechts vom Knick bei (0|4) gezeichnet werden.
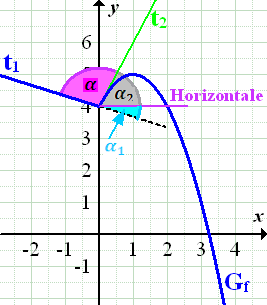
Abb.:Graph 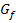mit 
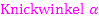zwischen den beiden Tangenten 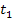und 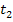, sowie die Winkel der Tangenten 
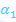und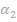 
jeweils gegenüber der Horizontalen
Betrachte nun die Abbildung und überlege dir, wo der vorher berechnete 81,86°-Winkel liegt! Bedenke dabei, was wir gerechnet haben, um ihn zu erhalten!
