Stetigkeit und Differenzierbarkeit
Achtung:Fertige vorweg auf jeden Fall eine Skizze an, die den Graphen der teilweise definierten Funktion und die beiden Tangenten an der Knickstelle zeigt! (Zeichne dabei die Tangenten jeweils als Halbgerade, d.h. als Linie, die an der Knickstelle endet, und nicht als komplett durchgezogene Gerade.) Nur mit Hilfe der Skizze kannst du erkennen, ob im konkreten Fall der gesuchte Knickwinkel spitz (kleiner als 90°) oder stumpf (zwischen 90° und 180°) ist. Der Knickwinkel kann nämlich im Einzelfall auch stumpf sein! Darin unterscheidet sich der Knickwinkel vom Schnittwinkel zweier Geraden.
Zur Erinnerung:Unter dem Schnittwinkel zweier Geraden versteht man grundsätzlich den kleineren der beiden Winkel, unter dem sich die zwei Geraden schneiden, also den spitzen Winkel.
Der gesuchte Knickwinkel ist jedoch der Winkel zwischen zwei Halbgeraden und der kann spitz oder stumpf sein! Mit der Formel 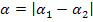 ergibt sich leider manchmal nur der Nebenwinkel des tatsächlichen Knickwinkels. Dann musst du dein Ergebnis noch von 180° abziehen. Ob du das im konkreten Fall tatsächlich machen musst, erkennst du am besten an der Skizze.
ergibt sich leider manchmal nur der Nebenwinkel des tatsächlichen Knickwinkels. Dann musst du dein Ergebnis noch von 180° abziehen. Ob du das im konkreten Fall tatsächlich machen musst, erkennst du am besten an der Skizze.
Wenn du an deiner Skizze erkennen kannst, dass der tatsächliche Knickwinkel spitz ist, du aber mit der Formel 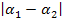 einen stumpfen Winkel erhalten hast, musst du dein Ergebnis noch von 180° abziehen. Das gleiche gilt, wenn du aus der Skizze schießt, dass der gesuchte Knickwinkel stumpf ist, du aber mit der Formel
einen stumpfen Winkel erhalten hast, musst du dein Ergebnis noch von 180° abziehen. Das gleiche gilt, wenn du aus der Skizze schießt, dass der gesuchte Knickwinkel stumpf ist, du aber mit der Formel 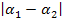 einen spitzen Winkel erhalten hast.
einen spitzen Winkel erhalten hast.
Wenn dir das mit dem spitzen und stumpfen Winkel noch nicht klar ist, solltest du jetzt nicht gleich aufgeben und dir denken „verstehe ich sowieso nicht“, sondern einfach die folgende Lösung unseres konkreten Beispiels anschauen. Dann wird dir bestimmt klar, wie du feststellen kannst, ob du dein Ergebnis am Schluss noch von 180° abziehen musst oder nicht.
Hier noch einmal unsere Funktion: 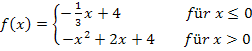
Bei der Überprüfung der Differenzierbarkeit haben wir die Grenzwerte der Ableitung an der Stelle 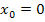 schon berechnet. Die Ergebnisse entsprechen den Steigungen
schon berechnet. Die Ergebnisse entsprechen den Steigungen 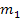 und
und 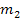 der Tangenten von links bzw. von rechts an der Knickstelle.
der Tangenten von links bzw. von rechts an der Knickstelle.


Berechnung des Winkels 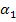 der linksseitigen Tangente gegenüber der Waagrechten:
der linksseitigen Tangente gegenüber der Waagrechten:
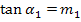
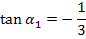
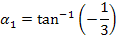
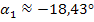
Berechnung des Winkels 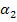 der rechtsseitigen Tangente gegenüber der Waagrechten:
der rechtsseitigen Tangente gegenüber der Waagrechten:
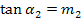

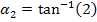
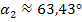
Berechnung des Differenzwinkels 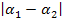
Entweder setzt du direkt in die Formel 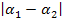 ein, oder du ziehst einfach vom größeren Winkel den kleineren ab.
ein, oder du ziehst einfach vom größeren Winkel den kleineren ab.

