Stetigkeit und Differenzierbarkeit
Genau das sollte ja auch gezeigt werden. Der Graph hat also einen Knick bei 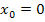 .
.
Berechnung des Knickwinkels
Auch für die Berechnung des Knickwinkels stehen uns zwei verschiedene Methoden zur Verfügung. Bei der einen Methode braucht man nur die Formel 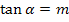 für den Schnittwinkel einer Geraden mit der x-Achse zu kennen. Diese Methode ist wohl für Gymnasiasten und Schüler einer FOS nichttechnischer Zweig die empfehlenswertere von beiden.
für den Schnittwinkel einer Geraden mit der x-Achse zu kennen. Diese Methode ist wohl für Gymnasiasten und Schüler einer FOS nichttechnischer Zweig die empfehlenswertere von beiden.
Die zweite Methode verwendet nämlich eine relativ komplizierte Formel (siehe unten) für den Schnittwinkel zweier Geraden, die zwar in der orangen bsv-Formelsammlung (früher zugelassen) und in der Merkhilfe für die FOS technischer Zweig steht, jedoch nicht mehr auf der aktuellen sehr knappen Merkhilfe für G8 oder FOS nichttechnischer Zweig. An sich muss man nur die Ergebnisse der Grenzwerte 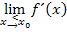 und
und 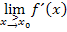 in die erwähnte, relativ komplizierte Formel einsetzen und mit dem Taschenrechner erhält man dann gleich in einem Schritt den Winkel zwischen den beiden Tangenten. Leider müssten sich Gymnasiasten und Schüler einer FOS nichttechnischer Zweig die erwähnte Formel auswendig merken, daher ist dieser Weg nur für Schüler einer FOS technischer Zweig zu empfehlen.
in die erwähnte, relativ komplizierte Formel einsetzen und mit dem Taschenrechner erhält man dann gleich in einem Schritt den Winkel zwischen den beiden Tangenten. Leider müssten sich Gymnasiasten und Schüler einer FOS nichttechnischer Zweig die erwähnte Formel auswendig merken, daher ist dieser Weg nur für Schüler einer FOS technischer Zweig zu empfehlen.
| Für alle Schüler eines Gymnasiums G8 und FOS nichttechnischer Zweig:
1. Methode zur Berechnung des Knickwinkels
Bei der Untersuchung der Differenzierbarkeit an der Stelle Wir bezeichnen die Ergebnisse dieser Grenzwerte mit
Mit der Formel D. h. mit dem Taschenrechner (im Mode DEG) Benötigte Tastenfolge: · Mit der Formel D. h. mit dem Taschenrechner (im Mode DEG) Benötigte Tastenfolge:
In Worten:Positiven Unterschied der Winkel Sind die Winkel Ist einer der Winkel Sind beide Winkel · Eventuell das berechnete Ergebnis noch von 180° abziehen. Ob das nötig ist, überlegst du dir in der konkreten Aufgabe am besten mit Hilfe einer Skizze. |

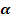 an der Stelle
an der Stelle 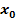
 wurden bereits die beiden Grenzwerte der Ableitung
wurden bereits die beiden Grenzwerte der Ableitung 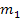 und
und 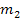 . Diese beiden Ergebnisse stellen die Tangentensteigungen von links bzw. von rechts dar.
. Diese beiden Ergebnisse stellen die Tangentensteigungen von links bzw. von rechts dar.
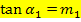 den Winkel
den Winkel 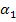 der linksseitigen Tangente gegenüber der Waagrechten berechnen.
der linksseitigen Tangente gegenüber der Waagrechten berechnen.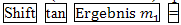
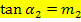 den Winkel
den Winkel 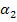 der rechtsseitigen Tangente gegenüber der Waagrechten berechnen.
der rechtsseitigen Tangente gegenüber der Waagrechten berechnen.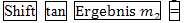

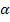 oder seinen Nebenwinkel (vergleiche unten!).
oder seinen Nebenwinkel (vergleiche unten!).