Stetigkeit und Differenzierbarkeit

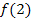wird gebildet, indem für x in die obere Teilfunktion 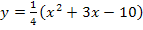die Zahl 2 eingesetzt wird. Bei 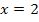gilt schließlich die obere Teilfunktion.

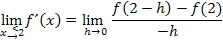
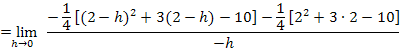
Die Klammer 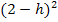löst man am schnellsten auf, indem man die zweite Binomische Formel 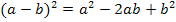anwendet.

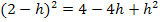
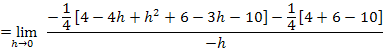
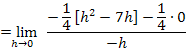
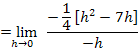
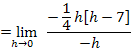
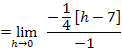
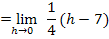
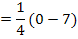
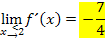
Hier noch einmal die betragsfreie Form der Funktion: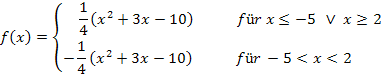

Nun weiter mit dem Grenzwert bei Annäherung an die Stelle 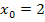von der rechten Seite:

Allgemeiner Ansatz für den rechtsseitigen Grenzwert der Ableitung:

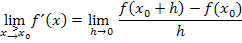
Wir überprüfen gerade die Differenzierbarkeit bei rechtsseitiger Annäherung an die Stelle 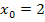. Daher setzen wir für die Zahl 2 in den allgemeinen Ansatz ein. So ergibt sich:

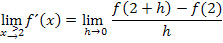
Da wir uns von rechts an die Stelle 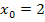annähern, brauchen wir diejenige Teilfunktion, die für 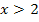gilt. Das ist die obere Teilfunktion 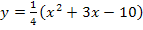. Um 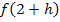zu bilden, muss jedes darin vorkommende x durch den Ausdruck 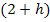ersetzt werden. 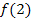wird gebildet, indem für x in die obere Teilfunktion die Zahl 2 eingesetzt wird. Die obere Teilfunktion gilt schließlich auch für .

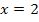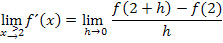
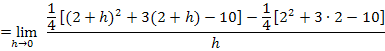
Die Klammer 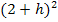löst man am schnellsten auf, indem man die erste Binomische Formel 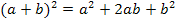anwendet:

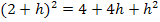
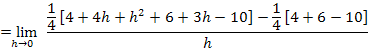
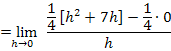
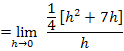
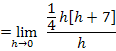
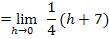
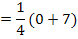
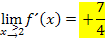
Zum Vergleich hier noch einmal der bereits vorher berechnete linksseitige Grenzwert:

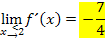
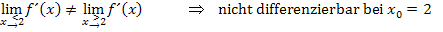
Dasselbe Ergebnis haben wir natürlich schon mit der 1. Methode erhalten.

Damit du dir das Ganze besser vorstellen kannst, hier noch einmal der Graph :

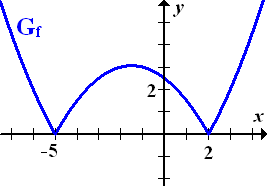
Abb.:Graph 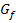der Funktion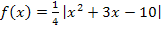

An diesem Beispiel wurde oben bereits erklärt, wie man Betragsfunktionen zeichnen kann, wenn der Betrag die gesamte Funktionsgleichung komplett umfasst. Halten wir noch einmal fest:

Zum Zeichnen von Betragsfunktionen

Eine Funktion, bei der die Betragsstriche den ganzen Ausdruck umschließen, lässt sich besonders leicht zeichnen. Man lässt erst einmal den Betrag weg und zeichnet den Graph dieser Funktion. Dann klappt man den unterhalb der x-Achse liegenden Teil bzw. die entsprechenden Teile des gezeichneten Graphen einfach nach oben. Man spiegelt also ausschließlich den Teil an der x-Achse nach oben, der unter der x-Achse liegt. Dadurch ergibt sich der Graph der entsprechenden Betragsfunktion.

Diesen Trick konnte man auch beim Zeichnen der Funktion 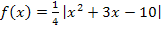verwenden, da sie sich auch folgendermaßen schreiben lässt:

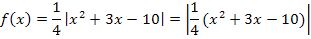
Dann umfasst der Betrag die komplette Funktion. Durch das Weglassen des Betrages, erhält man die Parabel 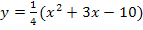. Man zeichnet zuerst die Parabel 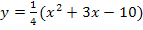und klappt dann den Teil des Graphen, der unterhalb der x-Achse verläuft, nach oben.

---