Stetigkeit und Differenzierbarkeit
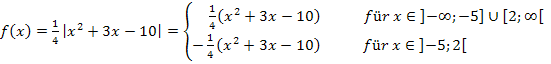
Wir beginnen mit der Untersuchung auf Differenzierbarkeit an der Stelle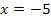 
. Diese Stelle nennen wir nun 
. Es gilt somit: 
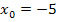
1. Methode:Ableitung der Teilfunktionen bilden und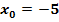 
einsetzen in beide Ableitungen
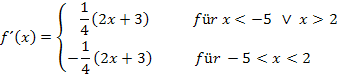
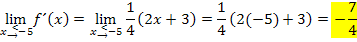
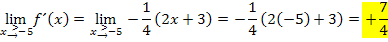
Die Ergebnisse sind nicht gleich, daher ist die Funktion 
an der Stelle 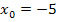nicht differenzierbar. Hier hat der Graph einen Knick. Außerdem sind die Vorzeichen der beiden Grenzwerte 
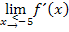und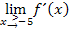 
unterschiedlich, so dass an der Stelle 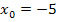ein Vorzeichenwechsel der ersten Ableitung vorliegt:Der Graph besitzt daher bei 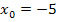ein Extremum, genauer gesagt einen absoluten Tiefpunkt. Dass es sich um einen Tiefpunkt handelt, erkennt man daran, dass 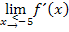negativ und 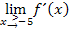positiv ist, also daran dass der Graph links von 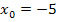fällt und direkt rechts davon steigt. (Er steigt jedoch nur bis 
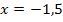. Dort verläuft die Tangente waagrecht und es ändert sich die Monotonie des Graphen wieder. Bei 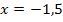ist ein relativer Hochpunkt von 
.)
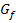2. Methode:Differenzierbarkeit untersuchen mit der h-Methode
Hier noch einmal die betragsfreie Form der Funktion: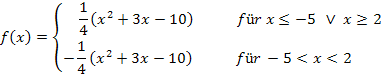 
Allgemeiner Ansatz für den linksseitigen Grenzwert der Ableitung:
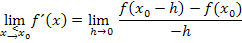
Wir überprüfen gerade die Differenzierbarkeit an der Stelle 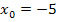. Daher setzen wir für die Zahl -5 in den allgemeinen Ansatz ein. So ergibt sich:
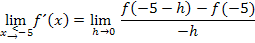
Da wir uns von links an die Stelle 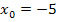annähern, brauchen wir diejenige Teilfunktion, die für 
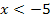gilt. Das ist die obere Teilfunktion 
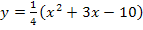. Um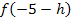 
zu bilden, muss jedes darin vorkommende x durch den Ausdruck 
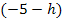ersetzt werden. 
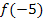wird gebildet, indem für x in die gleiche Teilfunktion -5 eingesetzt wird. Die obere Teilfunktion gilt schließlich auch bei .
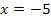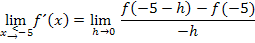
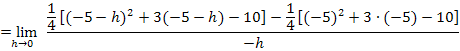
Die Klammer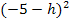 
löst man am schnellsten auf, indem man innerhalb der Klammer ein Minus ausklammert. Wegen des Quadrates außerhalb der Klammer fällt das Minus dann letztendlich weg: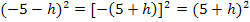 
Nun kann die erste Binomische Formel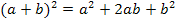 
angewendet werden, um die Klammer 
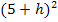aufzulösen: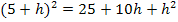 
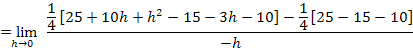
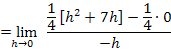
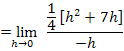
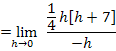
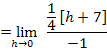
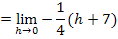
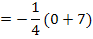
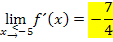
Hier noch einmal die betragsfreie Form der Funktion: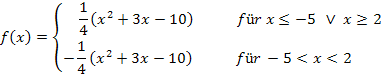
Allgemeiner Ansatz für den rechtsseitigen Grenzwert der Ableitung:
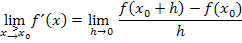
Wir überprüfen gerade die Differenzierbarkeit an der Stelle 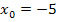. Daher setzen wir für die Zahl -5 in den allgemeinen Ansatz ein. So ergibt sich:
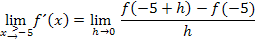
Da wir uns von rechts an die Stelle 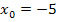annähern, brauchen wir diejenige Teilfunktion, die für 
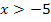gilt. Das ist die untere Teilfunktion 
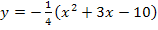. Um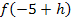 
zu bilden, muss jedes darin vorkommende x durch den Ausdruck 
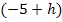ersetzt werden. 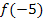wird gebildet, indem für x in die obere Teilfunktion -5 eingesetzt wird.
